Nexus7用HMDの解説
立体視の原理
まずは立体視の原理から確認してみましょう。
Googleで「立体視 原理」でググって下さい。
…さて、理解が出来たところで次に行きます。
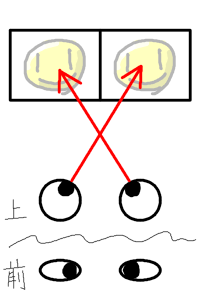
目玉の動き(視線の交差)
ではこの場合、視線と目玉の関係は…?
うん。私にはとても真似出来そうにありません。目が痛そうです。出来たとしてもなれない姿勢だから長時間やったらつかれそうです。
「こんな状況ふつう遭遇しないだろw」…だと?
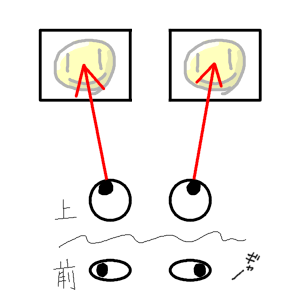
では平行法用の画像をサイズが異なるディスプレイで見た場合はどうなるでしょうか。

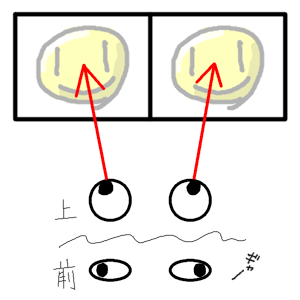
動画サイトに投稿されている平行法用の画像はスマホで見るのであれば立体視にちょうどいいのですが、家庭用テレビで同じように立体視するのはとうてい無理であることが容易に想像できると思います。 画面から離れれば負担は軽減できますが、離れた分だけ映像が小さくなります。
限界角度・限界距離
ではどれだけ映像を離すと目に負担がかかり始めるのか?
答えはこれです。

普段の生活の中で、視線が平行以上に広がることはありません。
ですので、これ以上離れれば目に負担がかかり始めます。
ではこの距離はいくつでしょうか?
これも絵の中に答えがありました。
目の黒い部分から目の黒い部分までの距離がそのまま左右の映像を離すことが出来る限界距離となります。(限界を多少超えても見えることは見える。疲れるけど。)
また同時にこれは平行法の映像として最適な距離とも言えるはずです。
この距離は「瞳孔間距離(Pupil Distance)」と呼ばれるそうです。
OculusRiftにもIPDの名称で設定欄が設けられているそうです。OculusRiftを持ってる人は取り敢えず64mmで設定したのではないでしょうか?
瞳孔間距離の具体的数値
瞳孔間距離は定規と鏡があれば自宅で簡単に計測できます。やり方はググってください。
成人での平均値は、男性で 64mm、女性 62mm だそうです。(信頼できる情報源は見つけられませんでしたが、大きくはズレていないでしょう。)
全画面表示になる立体視用アプリや動画を見てみると、どうやら「瞳孔間距離=ディスプレイ横幅の半分」で作っているようです。(遠景の部分に定規を当てて測った。)
設定できる項目なんてあるわけもないので瞳孔間距離はディスプレイサイズ依存になります。
本来ならば瞳孔間距離の設定項目付けるか、ディスプレイサイズと解像度から許容値内になるよう映像を補正してくれるべきです。そうでなければ環境によっては使いものになりません。その点Google Cardboardのサンプルアプリはよく出来ていますね。助かります。
Nexus7でHMDを作ったとすると横幅は151mmあるので、全画面表示した場合は瞳孔間距離が75.5mm必要ということになります。
151 / 2 = 75.5
目を左右に開いて11.5~13.5mm離れた場所を見る必要があります。片目だけで5.75~6.75mm。
瞳孔間距離 64mm の場合
75.5 - 64 = 11.5
11.5 / 2 = 5.75
瞳孔間距離 62mm の場合
75.5 - 62 = 13.5
13.5 / 2 = 6.75
HMDでは目の前の 数cm~10cm程度の近距離で見るため、かなり頑張らないといけなくなります。
解決方法
頑張らずに解決するにはどうすればよいか?
視線を曲げればいいんです。
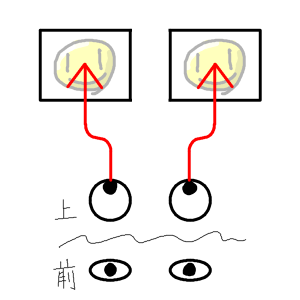
ガンバスターのホーミングレーザーのように、こう…ぐいっと、努力と根性で?
しかし残念ながら私は努力も根性も持ち合わせていないので、以下の2つの方法を思いついて検討しました。
鏡で2回反射させる方法と、
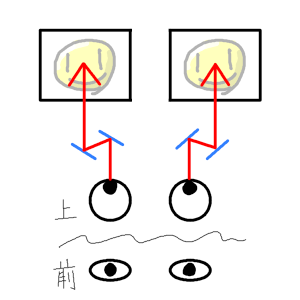
透明の板で屈折させる方法。
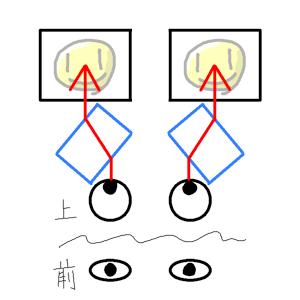
タブレットでHMD作りたいならスペースの関係上、透明の板で屈折させる方法が現実的です。
屈折率の計算
入射角、屈折角、屈折率についてはググってください。
こんな配置を想定して視点が移動する距離を算出してみましょう。
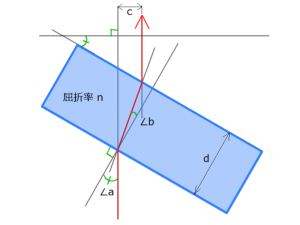
n:屈折率
a:入射角(透明板の設置角度)
b:屈折角
d:透明板の板厚
c:視線の推移距離
図のとおり屈折率が高いほうが移動距離も大きいので都合が良さそうです。まずは透明板の材料を選定しましょう。
入手が容易な素材で屈折率を調べてみました。
| 材質 | 屈折率 |
|---|---|
| 水 | 1.333 |
| アクリル樹脂 | 1.49 |
| 光学ガラス | 1.43 - 2.14 |
アクリルが屈折率も高く、加工も入手も手頃です。ということで材料はアクリル板に決定です。
材料も決まったことだし、設置角度や視点の移動距離を計算してみましょう。
まず入射角から屈折角を算出します。屈折率が、
![]()
なので、屈折角 b は、
![]()
ここからcを算出。
![]()
計算式があまり綺麗に整理できませんでした。
Excel使えば計算は簡単だからいいよねってことでお許し下さい。
幅 80mm のアクリル板(5mm厚)を積層した場合を想定して、どのくらいの設置角度にすればいいのか計算して表にまとめました。
| d [mm] | a [deg] (瞳孔間距離=64~62mm) (c=5.75~6.75 mm) | 奥行き [mm] |
|---|---|---|
| 60 | 16.2~18.8 | 84.4~88.6 |
| 55 | 17.6~20.4 | 81.3~85.8 |
| 50 | 19.2~22.2 | 78.6~83.4 |
| 45 | 21.1~24.4 | 76.4~81.5 |
| 40 | 23.5~27.0 | 74.6~80.0 |
| 35 | 26.4~30.2 | 73.5~79.2 |
| 30 | 30.0~34.2 | 73.2~79.3 |
| 25 | 34.8~39.3 | 74.1~80.4 |
| 20 | 41.2~46.1 | 76.3~82.7 |
| 15 | 50.2~55.6 | 80.3~86.6 |
| 10 | 64.5~70.8 | 86.0~92.4 |
「奥行き」はアクリル板を重ねて最適角度に設置した場合、設置に必要な奥行き寸法です。コンパクトな方がいいですよね。
これを見ると30mm(5mm厚の6枚重ね)が一番コンパクトで良さそうですが、差が大きいところでも 1cm 程度しか変わらないのであまり気にしなくても良さそうです。
人の工作精度は計算に入っていない
と、計算上はこのようになります。
しかし実際には、購入したアクリル板の屈折率が1.49になっているか確認が必要です。
また自分の瞳孔間距離の測定も必要です。
加工・工作精度の問題もあるでしょう。
付けてみるとちょっと調整したほうが焦点を合わせやすいということもあるかもしれません。
など色々とありますので、計算はあくまで参考値とお考え下さい。