浮力表現

2023/03/04

目次

はじめに 水面に箱が落ちるサンプル 箱に働く浮力 箱に働く水の抵抗 浮力と抗力の合力を適用 おきあがりこぼしを実装 応用 まとめ

はじめに

　ゲームフィールド内の通行禁止領域どうしよう？ 見えない壁というのも、通れるように見えて通れないのはストレス。 山や建物を置くか、他には…池とか？ 池を泳いで渡れば通り抜けはできるけど、結局正規ルートよりも時間がかかる。とかできると面白そう！ そういや、水に浮く表現ってやってなかったな。 計算式はわかってるし、作ってみるか。 …というわけで、作ってみました。

　HGIMG4には、直接浮力を表現できる命令は用意されていません。 ですが、gppapply命令でオブジェクトノードに力を加えることはできます。 そこで、液体中に物体を沈めた際の物体に働く力さえ算出して、オブジェクトノードに力として加える方法をとりました。

水面に箱が落ちるサンプル

　計算式を並べ立てるよりも、まずは動いているものを見た方がいいでしょう。先ずはサンプルです。 実行すると水色の水面に、上から箱が降ってきます。 箱が水中に落ちると、箱に浮力が発生して浮き上がってきます。

　箱は1 mの立方体。密度は、 0.1e+3 kg/m3（木材のバルサ相当）です。 浮力と水の抵抗は、箱と同質量の球形として簡易計算しています。

サンプルを実行すると水面に見立てた床に箱が浮かぶ


  #include "hgimg4.as"
  title "HGIMG4"
  
  ;	定数
  ; 重力加速度
  grav = 9.80665
  ; 水の密度 kg/m^3
  rhoWater = 1000.0
  ; 箱の抗力係数
  cd  = 0.5
  ; 箱の密度 kg/m^3
  ;rhoModel = 150.0	; 見た目がいい感じの密度
  ;rhoModel = 7.874e+3	; 鉄
  ;rhoModel = 0.968e+3	; ナトリウム
  ;rhoModel = 0.42e+3	; 木材（ヒノキ）
  rhoModel = 0.1e3	; 木材（バルサ）
  ;rhoModel = 30.0	; 発泡スチロール →収束しない！
  ;rhoModel = 0.917e+3	; 氷（0度）
  
  
  ;	環境作成
  gpreset
  setcls CLSMODE_SOLID, $808080
  
  ;	カメラ
  setpos   GPOBJ_CAMERA, 0, 2, 20
  gplookat GPOBJ_CAMERA, 0, 0.5, 0
  
  ;	箱を作成
  gptexmat id_texmat, "res/qbox.png"
  gpbox   id_model, 1.0, -1, id_texmat
  setpos  id_model, 0, 50, 0
  gppbind id_model, 500, 0.5
  
  ;	箱をクローン
  ; 見た目は箱ですが、浮力を計算する際は球形として簡易計算します。
  ; 球の半径は、箱の体積に一致する値を算出して使用します。
  
  ; 箱の体積
  v = powf(1.0, 3)
  
  ; 箱の体積と同じ球体の半径
  ; 球の体積＝4*π*r^3 / 3
  r_float = powf( v * 3.0 / (4.0 * M_PI), 1.0/3.0 )
  
  ; 箱同士がぶつからないように配置
  ; 物理設定も行う。
  ; 質量：v * rhoModel
  ddim posXYZ,  3, 100
  ddim posXYZ0, 3, 100
  i = 0
  d = 1.1
  repeat 10
    z = cnt
    repeat 10
      x = cnt
      gpclone id_models(i), id_model
      setpos  id_models(i), d*x-5.0, 12.0, d*z-5.0
      gppbind id_models(i), v * rhoModel, 0.5
      gppset  id_models(i), GPPSET_DAMPING, 0.1
      i++
    loop
  loop
  num_float = i
  
  
  ;	水面を作成
  gpfloor  id_floor, 30,50, $AFDFE4
  gpsetprm id_floor, PRMSET_ALPHA, 128
  
  ; 水面高さ
  py_floor = 0.0
  setpos id_floor, 0, py_floor,0
  
  ; 確認用変数
  ddim vel_y, 10
  ddim fu_y, 10
  ddim drag_y, 10
  
  
  *main
    stick key,15
    if key&128 : end
  
    ;-----------------------------
    ;	描画
    ;-----------------------------
    redraw 0
      gpdraw
  
      ;-----------------------------
      ;	クローン箱に加わる力を計算
      ;-----------------------------
      repeat num_float
        ; 位置
        posXYZ0(0,cnt) = posXYZ(0,cnt), posXYZ(1,cnt), posXYZ(2,cnt)
        getpos id_models(cnt), x, y, z
        posXYZ(0,cnt) = x, y, z
        
        ; 速度
        velX = posXYZ(0,cnt) - posXYZ0(0,cnt)
        velY = posXYZ(1,cnt) - posXYZ0(1,cnt)
        velZ = posXYZ(2,cnt) - posXYZ0(2,cnt)
        vel_y(cnt) = velY
        
        ; 箱中心からの水面位置
        py = py_floor - posXYZ(1,cnt)
    
        ;	空中と水没中での挙動を切り替え
        if py <= -r_float {
          ;	空中
          gppset id_models(cnt), GPPSET_DAMPING, 0.10, 0.10
  
          fu_y(cnt) = 0.0
          drag_y(cnt) = 0.0
          
        } else {
          ;	水没
          ; 水面に接している場合は、水没として判定します。
          gppset id_models(cnt), GPPSET_DAMPING, 0.8, 0.4
    
          ;---------------------
          ;	水中での浮力
          ;---------------------
          ; 水没している体積分に相当する水の質量が浮力になります。
          ; 球の水没した部分の計算式
          ;   https://keisan.casio.jp/exec/system/1166597867
          
          ; 水没部分の球の体積
          h = py + r_float
          h = limitf(h, 0.0, r_float * 2)
          c2 = h * (2.0 * r_float - h)
          vol = M_PI / 6.0 * h * (3.0 * c2 + h*h)
          
          ; 浮力
          f = rhoWater * vol * grav
          fu_y(cnt) = f
    
          ;---------------------
          ;	水の抵抗
          ;---------------------
          ; 抵抗は、速度の二乗に比例します。
          ; 抗力の式 F = 1.0 / 2.0 * rhoWater * v^2 * s * cd
          ; 抗力係数は物の形状やレイノルズ数などで変わるので、動作結果を見て調整する必要があります。
    
          ; 水平方向断面積
          ; 円の一部の面積：https://keisan.casio.jp/exec/system/1440724578
          ;t = 2.0 * acos(1.0 - h / r_float)
          a = 1.0 - h / r_float
          t = 2.0 *atan(sqrt(1.0-double(a)*(a)),(a))
          sh = t/2.0 * r_float * r_float - (r_float-h) * sqrt(h*(2.0*r_float-h))
    
          ; 垂直方向断面積
          if h >= r_float {
            r = r_float
          } else {
            r = sqrt(h * (2.0 * r_float - h))
          }
          sv = M_PI * r * r
          
          ; 抗力
          if velX > 0 : ax = -1.0 : else : ax = 1.0	; 方向
          if velY > 0 : ay = -1.0 : else : ay = 1.0
          if velZ > 0 : az = -1.0 : else : az = 1.0
          dv = 1.0 / 2.0 * rhoWater * sv * cd
          dh = 1.0 / 2.0 * rhoWater * sh * cd
          fx = ax * dh * velX * velX
          fy = ay * dv * velY * velY
          fz = az * dh * velZ * velZ
          drag_y(cnt) = fy
    
          ;---------------------
          ;	浮力と抵抗の合力			
          ;---------------------
          gppapply id_models(cnt), GPPAPPLY_FORCE, fx, fy+f, fz
        }
      loop
  
  
      color 255,255,255
      pos 8,8:mes "HGIMG4 sample"
  
      ;	デバッグ
      ; 数値表示
      if 0 {
        mes "        速度        浮力           抗力         合力        Y座標"
        repeat 10
          f = fu_y(cnt) + drag_y(cnt)
          m = strf( "(%d) %10.5f, %e + %10.5f = %10.3f ", cnt, vel_y(cnt), fu_y(cnt), drag_y(cnt), f )
          m+= strf( " %10.5f", posXYZ(1,cnt) )
          mes m
        loop
      }
      
    redraw 1
    await 1000/60
  
    ;デバッグ
    if 0 {
      if cnt_frame >= 0 {
        repeat
          gk0 = gk
          getkey gk, 32
          if (gk0 = 0) & (gk = 1) : break
          await 0
        loop
      }
      cnt_frame++
    }
  
    goto *main

　箱の密度は、変数rhoModelで指定しています。 箱の密度が、水の密度1000 kg/m3未満であれば、箱は浮いてきます。箱の密度が水の密度に近いほど浮き上る速度がゆっくりになります。 水の抵抗も計算しているため、水中での速度が速いほど止まろうとする力が大きく働きます。

　箱の密度が軽すぎると、動作が発散してしまうことがあります。 軽すぎると水中にとどまる時間が短いため、抵抗の計算が十分に反映されないことがあるようです。 本来なら抵抗で減速されてから水面から飛び出すはずが、減速が不十分なまま飛び出すために動作が発散してしまっています。 厳密な計算による対処は今のところ難しそうなので、GPPSET_DAMPINGなどで数値をうまく調整して対処してください。

箱に働く浮力

　物を水中に沈めると、浮かび上がろうとする力「浮力」が発生します。 物体が水を押しのけている質量分が浮力になります。アルキメデスの原理というやつです。 計算は簡単で、水の密度をρ[kg/m3]、物体の体積をV[m3]、重力加速度をg[m/s2]、浮力の大きさをF[N]とすると次のような計算式で算出できます。

F = ρVg

　水の密度と重力加速度は定数なので、体積を求めれば力を求めることができます。 中心座標が水面高さ以下になった瞬間、球体体積分の浮力が発生する…としてしまうと、箱の中心がちょうど水面付近で浮かんだ場合は、振動が収束しなさそうです。 これでは困るので、もう少し厳密に求めてみました。箱の一部だけが水につかっている場合は、水につかっている部分だけで浮力を計算します。

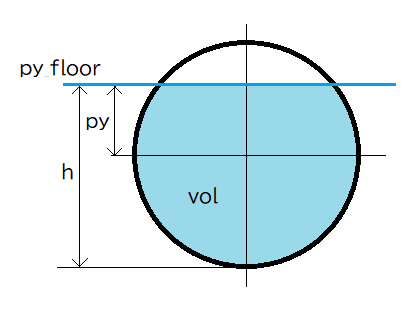
　まずは変数を定義します。図の青い水平ラインが水面、水色で塗っている部分が水没している部分です。 水色で塗っている部分の体積をvolとしています。

変数py_floor,h,py,vol

py_floor
水面高さ
h
球の底部から水面までの高さ
py
球の中心から水面までの高さ
vol
球面が水につかっている部分の体積

　球の体積の計算式は導出がめんどくさいので、こちらを参考にしました。書き写すだけなので簡単な作業です。

keisan 一部が欠けた球の体積
https://keisan.casio.jp/exec/system/1166597867

なお、算出された浮力は、重力と反対方向…つまり+Y方向に働きます。 


  ; 水没部分の球の体積
  h = py + r_float
  h = limitf(h, 0.0, r_float * 2)
  c2 = h * (2.0 * r_float - h)
  vol = M_PI / 6.0 * h * (3.0 * c2 + h*h)
  
  ; 浮力
  f = rhoWater * vol * grav

箱に働く水の抵抗

　物体が水中を移動すると、物体が進む方向と逆方向に水からの抵抗を受けます。 抵抗の大きさは速度の二乗に比例します。 計算式を書くと次のようになります。

D = 1/2 ρ V2S Cd

  • D ：抗力 Drag [N]
  • ρ：流体の密度 Pressure [kg/m^3]
  • V ：代表速度 Velocity [m/s]
  • S ：代表面積 Surface [m^2]
  • Cd：抗力係数 Coefficient of Drag [-]

　代表速度はこの場合、物体の移動速度です。 代表面積には通常は、移動方向から見た投影面積が使用されます。 抗力係数は、物体の形状や大きさ、向きによって変わります。このサンプルでは、適当に0.5としました。

　ということなので、面積が決まれば抗力が計算できそうです。 完全に水没してした場合の投影面積は、球を中心でふたつに切った際の断面積と同じなので、円の面積計算で簡単に算出できます。 しかし一部が水面から外に出ている場合は、球の深度で投影面積が変わってきます。何より横から見ると円形ではないので、計算式を求める必要があります。 ここでは導出は目的ではないので、keisanを探してみます。

keisan 弓形の面積（弓形の半径と高さから）
https://keisan.casio.jp/exec/system/1440724578

　いいのがありました。 これで水平方向の投影面積は算出できます。垂直方向の投影面積も、弦の長さCから算出できました。

　算出した抗力は、方向情報を持っていない力の大きさです。 抗力は速度方向と逆方向に働くので、最後に方向情報を加えます。 


  ; 方向
  if velX > 0 : ax = -1.0 : else : ax = 1.0
  if velY > 0 : ay = -1.0 : else : ay = 1.0
  if velZ > 0 : az = -1.0 : else : az = 1.0
  ; 抗力
  dv = 1.0 / 2.0 * rhoWater * sv * cd
  dh = 1.0 / 2.0 * rhoWater * sh * cd
  fx = ax * dh * velX * velX
  fy = ay * dv * velY * velY
  fz = az * dh * velZ * velZ

浮力と抗力の合力を適用

　算出した浮力と抗力の合力を箱に加えます。 


  gppapply id_models(cnt), GPPAPPLY_FORCE, fx, fy+f, fz

　しかしこれだけだと、無限に水面を跳ねるだけになってしまいます。 抗力係数を大きくしてもいいのですが、この例ではGPPSET_DAMPINGを調整しました。

　箱が水に接している場合は減衰を大きくし、空中にいる間は減衰が小さい元の値に戻します。 


  gppset id_models(cnt), GPPSET_DAMPING, 0.8, 0.4

　これでずいぶん現実的な動きになってくれました。

おきあがりこぼしを実装

　水に浮いている物体は、形にもよりますがおおむね重心を下にして浮かびます。 前述したサンプルは、中心＝重心だったのであまり気になりませんでした。 しかし、ゲームだと船やアヒルなどは必ず頭が上になるような、決まった上下姿勢に収束してほしい場合がほとんどです。

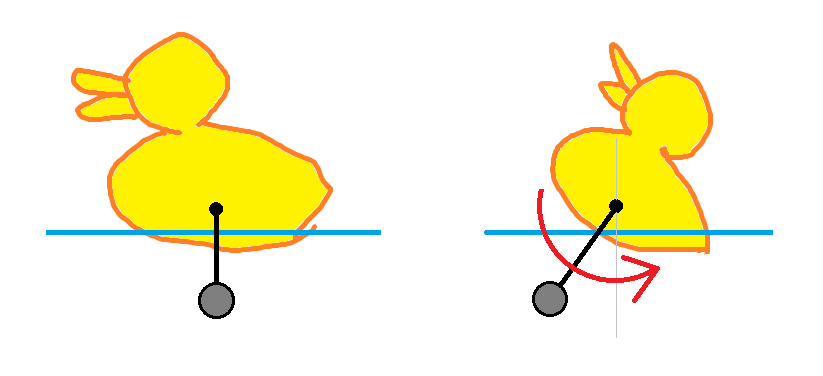
　ということで、おきあがりこぼしのように自然と起き上がる仕組みを入れてみたいと思います。 構造は簡単で、ノードオブジェクトの中心位置から、重心を下にずらすだけです。

下に錘をつけて重心を下げる

具体的には、ノードオブジェクトの少し下の座標に質量を取り付けて、ノードが傾くと元の姿勢に戻ろうとするモーメントが発生する仕組みです。 現実世界と同じ簡単な構造です。ノードが箱では、上下がわかりにくいので、アヒルに代わってもらうことにします。

サンプルを実行すると水面に見立てた床にアヒルが浮かぶ


  #include "hgimg4.as"
  #module
  #deffunc fvdir2 array v_fv, double p_rx, double p_ry, double p_rz
    ddim r, 3
    r = -p_rx, -p_ry, -p_rz
    fvdir r, v_fv(0), v_fv(1), v_fv(2)
    v_fv = r(0), r(1), r(2)
    return
  #global
  
  title "HGIMG4"
  
  ;	定数
  ; 重力加速度
  grav = 9.80665
  ; 水の密度 kg/m^3
  rhoWater = 1000.0
  ; アヒルの抗力係数
  cd  = 0.5
  ; アヒルの密度 kg/m^3
  rhoModel = 150.0
  ; 仮想錘の位置
  ; 3Dモデルの中心座標からの相対座標を指定します。
  posMass = 0.0, -0.5, 0.0
  ; 仮想錘の重さ
  kgMass = 5.0
  
  
  ;	環境作成
  gpreset
  setcls CLSMODE_SOLID, $808080
  
  ;	カメラ
  setpos   GPOBJ_CAMERA, 0, 5, 20
  gplookat GPOBJ_CAMERA, 0, 0.5, 0
  
  
  ;	アヒルを作成
  gpload id_model, "res/duck"
  setpos  id_model, 0.5, 40, 1.5
  gppbind id_model, 20, 0.5, GPPBIND_MESH
  
  ;	アヒルをクローン
  ; 見た目はアヒルですが、浮力を計算する際は、球形として簡易計算します。

  ; アヒル半径
  r_float = 0.5
  v = 4.0 * M_PI * powf(r_float, 3.0) / 3.0
  
  ddim posXYZ,  3, 100
  ddim posXYZ0, 3, 100
  i = 0
  d = 1.7
  repeat 10
    z = cnt
    repeat 10
      x = cnt
      gpclone id_models(i), id_model
      setpos  id_models(i), d*x-7.0, 10.0, d*z-7.0
      gppbind id_models(i), v * rhoModel, 0.5, GPPBIND_MESH		; 80kg
      gppset  id_models(i), GPPSET_DAMPING, 0.1
      i++
    loop
  loop
  num_float = i
  
  ; かき混ぜるために大きい箱を落とす
  gptexmat id_texmat, "res/qbox.png"
  gpbox   id_model, 5.0, -1, id_texmat
  setang  id_model, deg2rad(30), 0.0, deg2rad(30)
  setpos  id_model,	0, 200, 0
  gppbind id_model, 500, 0.5, GPPBIND_MESH
  
  
  ;	水面を作成
  gpfloor  id_floor, 30,50, $AFDFE4
  gpsetprm id_floor, PRMSET_ALPHA, 128
  
  ; 水面高さ
  py_floor = 0.0
  setpos id_floor, 0, py_floor,0
  
  
  *main
    stick key,15
    if key&128 : end
  
    ;-----------------------------
    ;	描画
    ;-----------------------------
    redraw 0
      gpdraw
  
      ;-----------------------------
      ;	クローン アヒルに加わる力を計算
      ;-----------------------------
      repeat num_float
        ; 位置
        posXYZ0(0,cnt) = posXYZ(0,cnt), posXYZ(1,cnt), posXYZ(2,cnt)
        getpos id_models(cnt), x, y, z
        posXYZ(0,cnt) = x, y, z
        ; 速度
        velX = posXYZ(0,cnt) - posXYZ0(0,cnt)
        velY = posXYZ(1,cnt) - posXYZ0(1,cnt)
        velZ = posXYZ(2,cnt) - posXYZ0(2,cnt)
        
        ; アヒル中心からの水面位置
        py = py_floor - posXYZ(1,cnt)
  
        ;	空中と水没中での挙動を切り替え
        if py <= -r_float {
          ;	空中
          gppset id_models(cnt), GPPSET_DAMPING, 0.10, 0.10
        } else {
          ;	水没
          ; 水面に接している場合は、水没として判定します。
          gppset id_models(cnt), GPPSET_DAMPING, 0.8, 0.4
  
          ;---------------------
          ;	水中での浮力
          ;---------------------
          ; 水没している体積分に相当する水の質量が浮力になります。
          ; 球の水没した部分の計算式
          ;   https://keisan.casio.jp/exec/system/1166597867
          
          ; 水没部分の球の体積
          h = py + r_float
          h = limitf(h, 0.0, r_float * 2)
          c2 = h * (2.0 * r_float - h)
          vol = M_PI / 6.0 * h * (3.0 * c2 + h*h)
          
          ; 浮力
          f = rhoWater * vol * grav
  
          ;---------------------
          ;	水の抵抗
          ;---------------------
          ; 抵抗は、速度の二乗に比例します。
          ; 抗力の式 F = 1.0 / 2.0 * rhoWater * v^2 * s * cd
          ; 抗力係数は物の形状やレイノルズ数などで変わるので、動作結果を見て調整する必要があります。
  
          ; 水平方向断面積
          ; 円の一部の面積：https://keisan.casio.jp/exec/system/1440724578
          ;t = 2.0 * acos(1.0 - h / r_float)
          a = 1.0 - h / r_float
          t = 2.0 *atan(sqrt(1.0-double(a)*(a)),(a))
          sh = t/2.0 * r_float * r_float - (r_float-h) * sqrt(h*(2.0*r_float-h))
  
          ; 垂直方向断面積
          if h >= r_float {
            r = r_float
          } else {
            r = sqrt(h * (2.0 * r_float - h))
          }
          sv = M_PI * r * r
          
          ; 抗力
          if velX > 0 : ax = -1.0 : else : ax = 1.0	; 方向
          if velY > 0 : ay = -1.0 : else : ay = 1.0
          if velZ > 0 : az = -1.0 : else : az = 1.0
          dv = 1.0 / 2.0 * rhoWater * sv * cd
          dh = 1.0 / 2.0 * rhoWater * sh * cd
          fx = ax * dh * velX * velX
          fy = ay * dv * velY * velY
          fz = az * dh * velZ * velZ
  
          ;---------------------
          ;	浮力と抵抗の合力			
          ;---------------------
          gppapply id_models(cnt), GPPAPPLY_FORCE, fx, fy+f, fz
        }
  
  
        ;---------------------
        ;	重心をずらす仮想錘
        ;---------------------
        ; おきあがりこぼしのように起き上がるようになります。
        ; 錘座標
        fvset fv, posMass(0), posMass(1), posMass(2)
        ; 中心から錘までの距離
        fv_abs = sqrt(fv(0)*fv(0) + fv(1)*fv(1) + fv(2)*fv(2))
        ; 現在の錘位置
        getang id_models(cnt), x,y,z
        fvdir2 fv, x,y,z
        ; 錘が3Dモデルに与えている力
        f = kgMass * grav
        ; 錘がノードオブジェクトに加えるモーメントを加える
        ; 力は必ず-Y軸方向に加わると仮定して計算しています。
        ; X軸方向とZ軸方向に分けて計算しています。
        gppapply id_models(cnt), GPPAPPLY_TORQUE, fv(2) * f, 0.0, fv(0) * -f
  
      loop
  
    
      color 255,255,255
      pos 8,8:mes "HGIMG4 sample"
  
    redraw 1
    await 1000/60
  
    goto *main

　少し遅れて大きめの箱を落として、アヒルに動きをつけてみました。かき混ぜるには、適当に少し傾けておくのがコツ。適度にばらけつつひっくり返ってくれました。 時間がたつと、すべてのアヒルが起き上がっています。成功です。

　実装方法を見ていきます。 スクリプトは、先ほどの箱を落とす場合とほぼ同じです。 追加したのは、「重心をずらす仮想錘」の部分になります。

　まず、動く前のアヒルの中心座標から錘（おもり）までの相対座標fvを作ります。fvの長さfv_absも後で使うので計算しておきます。 


  ; 錘座標
  fvset fv, posMass(0), posMass(1), posMass(2)
  ; 中心から錘までの距離
  fv_abs = sqrt(fv(0)*fv(0) + fv(1)*fv(1) + fv(2)*fv(2))

　アヒルが傾いているので、錘の相対座標も一緒に動いています。今の錘の相対座標を計算します。 


  ; 現在の錘位置
  getang id_models(cnt), x,y,z
  fvdir2 fv, x,y,z

　錘がアヒルに与えているモーメントを計算します。 前提として、錘が生む力は必ず-Y軸方向に加わると仮定します。
X軸回りのモーメントは、Z軸方向の距離×力となります。
Z軸回りのモーメントは、-X軸方向の距離×力となります。Z軸回りはプラスとマイナスが逆にしないと正しい回転方向にならないので注意。
Y軸回りには力が発生しないので、モーメントは常に0.0です。 


  ; 錘が3Dモデルに与えている力
  f = kgMass * grav
  ; 錘がノードオブジェクトに加えるモーメントを加える
  ; 力は必ず-Y軸方向に加わると仮定して計算しています。
  ; X軸方向とZ軸方向に分けて計算しています。
  gppapply id_models(cnt), GPPAPPLY_TORQUE, fv(2) * f, 0.0, fv(0) * -f

　この機能は、水上じゃなくても活用できる状況がありそうですね。

応用

　例えば板状のモデルの四つ角に、先ほどの浮力＋抗力を取り付けると、かなり船らしい動きをするそうです。 しかしHGIMG4はノードオブジェクトの中心座標に対して力を加える命令はありますが、ノードオブジェクトの任意のローカル座標点に力を加える命令はありません。 先ほどの実装を上手く使えば出来そうですが…まあ、使う予定もないのでまた気が向いたときに。

　あとは波が再現できれば、より現実っぽくできそうです。波の発生位置が動かず、数も少なく、岸などでの反射等がなく、波に変化がなければ、水面高さをsinで計算するだけなので簡単そうです。 すでにかなり限定的。海洋の再現なら簡単かな？いやしかしそうなると波のモデルもリアルに再現しないと…。

　作りこもうと思えば、いくらでもやることがありそうなのでやめておきます。(´・ω・｀)

まとめ

　浮力と抗力、減衰で、いい感じの物体が水面に浮く動きが再現できました。 しかし箱の質量が小さいと上手くいきませんね。浮くのが速すぎて抗力での減速がうまく計算しきれないまま、水面から飛び出しているようです。減衰で調整かな。

　さらに疑似的な錘を付けることで、起き上がる仕組みも作ることができました。 水に浮く表現では必須ではないものの、組み込むとより本物らしい表現になります。 陸上でも応用できそうなのがいいですね。

　しかしまあ…いろいろと計算をやってはいますが、それよりも水面のエフェクトや水しぶき演出を見せるだけの方がゲーム的には水らしく見えると思います。

関連記事

  1. 地表を歩く　地表を歩かせよう サンプル 大まかな手順 gppraytest 地面に垂直な線分 線分と地面モデルと...
  2. 物理挙動への制約　はじめに 回転 移動 摩擦 シーソーとすり抜け シーソーのを元の姿勢に戻す まとめ 　物理挙動は設定...