追跡
目次
はじめに
自機の後ろをNPCが追跡するプログラムを考えてみます。たとえば、次のような状況を想定したものです。
- シューティングゲームで支援機が自機をついてくる。
- シューティングゲームの追尾ミサイル。
- 昔のRPGのようにPCの後ろを仲間が付いてくる。
いろんなやり方があるので、ここで理想としているゴールは次の通りです。
- 自機を追跡機が追跡する。
- 追跡側は、自機の軌道と全く同じ軌道を通る。
- 自機と追跡側は、常に一定以上の距離を空ける。
実装が簡単ないくつかのパターンについて考えてみたので、順に紹介していきます。 どれも一長一短あって、結局正解は見つかっていません。いろいろ手はあるよという紹介です。
紹介するにあたって、共通項目をあらかじめ説明しておくことにします。 追跡される側となる自機の座標は、次のように設定します。手っ取り早くマウス座標です。 速度も方向も安定しませんが気にしない。
; 自機座標
mx = double(mousex)
my = double(mousey)
追跡するNPCの座標は、変数(sx, sy)を使います。
また、移動速度は、変数(vx, vy)です。ここで言う速度の単位は、[dot/frame]と定義しています。
NPCを移動するには、フレーム毎に次のようにしています。。
sx += vx
sy += vy
追尾
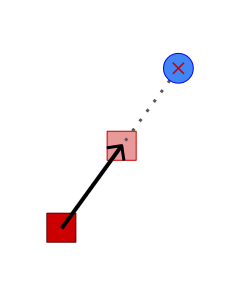
NPCは常に自機の方向を向いてまっすぐ一定速度で進みます。自機が動けば、それに合わせて方向を変えて、その方向にまっすぐ一定速度で進みます。 シンプルな挙動なので、実装が簡単でよく使われる方法だと思います。
言葉だけでは伝わらないので、まずはサンプルスクリプトを掲載します。解説はこの後。
; 敵を追い続けるミサイルのように、自機を追尾します。
; 一定速度で、常に自機の方向に向かって移動し続けます。
sx = 0.0
sy = 0.0
v0 = 5.0
*main
redraw 1 : await 16 : redraw 0 : color 255, 255, 255 : boxf : color : pos 0,0
; 自機座標
mx = double(mousex)
my = double(mousey)
; ------------------------------
; 追跡座標
; ------------------------------
; 追跡目標座標
; 自機を目標に追いかけます。
tx = mx
ty = my
; 追尾目標方向
lx = tx - sx
ly = ty - sy
l = sqrt(lx * lx + ly * ly) ; 距離
if l > 0.0 { ; ゼロ除算対策
; 移動速度より距離が近いと目標点を通り過ぎてしまいます。
; 通り過ぎて戻ろうとする動きを永遠に続けてしまいます。
; ここでの対策として、1フレーム後に目標点にぴったり一致する速度にしています。
v = v0
if l < v : v = l
; 方向ベクトル / 距離 で、方向単位ベクトルを算出。
; これを速度倍して、移動する方向と速度を算出。
vx = lx / l * v
vy = ly / l * v
; 移動後座標
; ここでの速度の単位の定義は、[ドット/フレーム]です。
; 次の座標=現在座標+速度×時間
; 時間:経過フレーム数。1フレームなので省略。
sx += vx
sy += vy
}
; ------------------------------
; 描画
; ------------------------------
; 自機
r = 5
color 0, 0, 255
circle mx-r, my-r, mx+r, my+r
; 追尾
color 255, 0, 0
circle sx-r, sy-r, sx+r, sy+r
color
line mx, my, sx, sy
goto *main
まず、NPCが追跡する際の目標点を、自機に設定します。
tx = mx
ty = my
次にNPCから見た目標点までの方向と距離が必要なので調べます。
; 追尾目標方向
lx = tx - sx
ly = ty - sy
l = sqrt(lx * lx + ly * ly) ; 距離
これで、進む方向が決まりました。(lx, ly)方向です。
次は、NPC移動速度を決めます。速度はある一定速度にしたいのですが、実際には動かすにはX方向の速度とY方向の速度に分ける必要があります。
方向ベクトル(lx, ly)を距離 l で割って単位ベクトルにします。あとは移動速度をかけてあげれば、方向ベクトルから速度ベクトルに変換できます。
lがゼロだと困るので、ゼロ割対策をしています。
vx = lx / l * v
vy = ly / l * v
実際にこれを動かすと、最初はいい感じに追いかけてくれます。追いついた瞬間振動がががが…。
NPCが自機に追いつく最後の瞬間、NPCは自機を追い抜いてしまいます。 次のフレームでは戻ろうとしますが、速度が大きすぎてNPCをまた通過してしまいます。最終的に自機の位置で止まることができずに、自機を中心に振動してしまいます。 自機に近づいたら、程よく減速する必要がありますね。
v = v0
if l < v : v = l
NPCから自機までの距離 l が、既定の移動速度 v0 よりも小さくなった場合、移動速度を l にします。
これならNPCは最後のフレームで、自機と同じ座標に移動できます。
けん引
追尾型はシンプルな構造なので作りやすいのですが、攻撃向きというか、後ろをついてきてくれる仲間という感じがありません。 自機にとびかかってくる点や一定の距離を保ってくれない点でしょうか。移動速度も合わせてくれません。
この章のサンプルです。
; 自機と追跡側が棒や紐で連結されたような動作をします。
; 棒や紐なので、一定距離以上離れることがありません。
sx = 0.0
sy = 0.0
v0 = 5.0
arm = 50.0
*main
redraw 1 : await 16 : redraw 0 : color 255, 255, 255 : boxf : color : pos 0,0
; 自機座標
mx = double(mousex)
my = double(mousey)
; ------------------------------
; 追跡座標
; ------------------------------
; 追跡目標座標
; 自機を目標に追いかけます。
tx = mx
ty = my
; 追跡目標から見た追尾側方向
lx = sx - tx
ly = sy - ty
l = sqrt(lx * lx + ly * ly) ; 距離
; 牽引されている点の座標を計算
; if l > arm { ; 紐
if l ! 0 { ; 固い梁
; 移動後座標
; ターゲット(mx,my)から既定の長さ距離の位置に移動
sx = lx / l * arm + tx
sy = ly / l * arm + ty
}
; ------------------------------
; 描画
; ------------------------------
; 自機
r = 5
color 0, 0, 255
circle mx-r, my-r, mx+r, my+r
; 追尾
color 255, 0, 0
circle sx-r, sy-r, sx+r, sy+r
color
line mx, my, sx, sy
goto *main
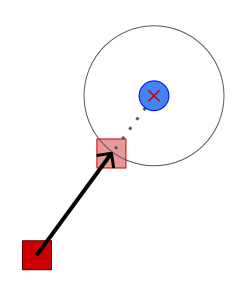
とにかく、一定の距離を保つ方法を考えてみました。 追尾される側から見て距離が一定になればいいんです。
; 目標から見た追尾側方向
lx = sx - tx
ly = sy - ty
この方向で、距離が一定値 arm になる位置に追跡側がいてほしいので、こうします。
if l ! 0 {
sx = lx / l * arm + tx
sy = ly / l * arm + ty
}
速度を出さずに追跡側座標が出てきましたが、これで一定の距離を保つようになります。 速度が欲しければ、逆算すればいいだけなので問題ないでしょう。
if l ! 0 { は、ゼロ割対策ですが、こう書き換えると違った動きをするようになります。
if l > arm {
sx = lx / l * arm + tx
sy = ly / l * arm + ty
}
自機を追跡側に近づけてみると、固い棒でつながっている動きから、ロープでつながっているような動きに変わっているのが分かります。
このように、レッカー車のように牽引(けんいん)するような動作をするので、タイトルをけん引にしたのですが…何と呼ぶのが正解かは分かりません。
ばねとダンパ
こういった連結機構を考えるときによく出てくる物の一つに「ばねとダンパ」があると思います。 物理シミュレーション系では、なじみ深いかもしれません。 ということで、作ってみました。
自機と追跡側を「ばねとダンパ」(サスペンション)で連結します。ばね(spring)は、引っ張ると伸びて、長さが伸びると元の長さに戻ろうとする仕組みです。 ダンパ(damper)は、ショックアブソーバーともいわれます。速度を減速する装置だと思ってください。 ばねだけでつなぐと永遠に振動し続けてしまうので、ダンパで減速させることで振動をゆっくり止めます。 また、ダンパは速度が速いほど減速する力が大きくなります。 水の中をゆっくり歩くことは簡単なのに、走ろうとすると難しいですよね。あのような性質があります。
このバネとダンパで自機と追跡側をつなぐと、独特の動きをするようになります。
見ながらかつ触りながらじゃないと分かりにくいので、サンプルをどうぞ。
; 自機と追尾側をバネとダンパで連結したサンプルです。
; バネでつながっているので、自機を中心に振動します。
; ダンパーでつながっているので、動きは徐々に小さくなっていきます。
;
sx = 0.0
sy = 0.0
vx = 0.0
vy = 0.0
; ばねダンパのパラメータ
prmK = 0.02741 ; ばね定数
prmD = 0.2 ; 減衰
prmMass = 10.0 ; 質量
; 限界減衰率
; 減衰をこの値より小さくすると、振動しながら収束するようになります。
; 減衰をこの値より大きくすると、振動せずに収束しますが、大きすぎるとなかなか目標点に到達できません。
cc = 2.0 * sqrt( prmMass * prmK)
;prmD = cc
; 減衰比
; この値を調べることで、振動がどのような挙動で減衰していくかが分かります。
; ζ<1 : 振動しながら収束
; ζ=1 : 緩やかに収束(一番いい感じの値)
; ζ>1 : おおきいほど緩やかに収束
zeta = prmD / cc
; 振動角周波数
; 振動周波数を求めるための途中経過の値です。
; ω = √(K/m)
w = sqrt(prmK / prmMass)
; 振動周波数
; 1秒間に何回振動するかを示す値です。次式から求めます。
; ω = 2πf
; 出てくる値は、フレームあたりの回数なので、1秒あたりに変換
freq = w / (2.0 * M_PI) * 60.0
*main
redraw 1 : await 16 : redraw 0 : color 255, 255, 255 : boxf : color : pos 0,0
; 自機座標
mx = double(mousex)
my = double(mousey)
; ------------------------------
; 追跡座標
; ------------------------------
; 追跡目標座標
; 自機を目標に追いかけます。
tx = mx
ty = my
; 目標から見た追跡側方向
lx = sx - tx
ly = sy - ty
l = sqrt(lx * lx + ly * ly) ; 距離
if l > 0.1 { ; 無限振動対策
; 距離が近くなると振動がなかなか収まらないので、
; 一定距離まで近づいたら、計算しないようにしています。
; ばね・ダンパ
; 方向ごとに速度を計算します。
; 力
fx = - prmK * lx - prmD * vx
fy = - prmK * ly - prmD * vy
; 速度=加速度+前回速度
vx = fx / prmMass + vx
vy = fy / prmMass + vy
; 移動後座標
; ここでの速度の単位の定義は、[ドット/フレーム]です。
; 次の座標=現在座標+速度×時間
; 時間:経過フレーム数。1フレームなので省略。
sx += vx
sy += vy
}
; ------------------------------
; 描画
; ------------------------------
; 自機
r = 5
color 0, 0, 255
circle mx-r, my-r, mx+r, my+r
; 追尾
color 255, 0, 0
circle sx-r, sy-r, sx+r, sy+r
; 連結部分
color
line mx, my, sx, sy
; パラメータ
pos 10, 10
mes "ばね定数:" + prmK
mes "減衰 :" + prmD
mes "質量 :" + prmMass
mes "限界減衰率Cc:" + cc
mes "減衰比 ζ :" + zeta
mes "振動角周波数:" + (w * 60.0) + " rad/sec"
mes "振動周波数 :" + freq + " Hz"
goto *main
まずは、計算に必要な条件を設定します。この値のバランスが難しいのですが、まずは値の意味と性質を解説します。
ばね定数は、バネの固さを表す値です。値が大きいほど固いバネになり、逆に小さいほどやわらかいバネになって振動がゆっくりになります。
減衰は、ダンパの強さを表す値です。値が大きいほど大きく減速し、小さいとなかなか減速しなくなります。
質量は、追尾側の重さです。値が大きい(重い)と動きがゆっくりになり、値が小さいと(軽い)と動きが速くなります。
; ばねダンパのパラメータ
prmK = 0.02741 ; ばね定数
prmD = 0.2 ; 減衰
prmMass = 10.0 ; 質量
学校で習う範囲というか、実生活でもなじみがあるので飲み込みやすいかなと思います。 しかし、このパラメータらから座標算出となると、あまりなじみがありません。といっても高校までに習う範囲です。
まずバネがどのくらい引っ張られているかがほしいので、距離を出します。
lx = sx - tx
ly = sy - ty
ばねダンパの運動方程式はこんな感じの式です。
ma + cv + kx = 0
m:質量
a:加速度
c:減衰
v:速度
k:ばね定数
x:ばねが伸びた長さ
この式から力 ma を求めて、
; 力
fx = - prmK * lx - prmD * vx
fy = - prmK * ly - prmD * vy
力 maから加速度 a を求めて、加速度 a から速度を求めます。 ここで出てくる加速度 a は、1フレームあたりの速度変化なので現在速度に加算すると次の速度が出せます。
; 速度=加速度+前回速度
vx = fx / prmMass + vx
vy = fy / prmMass + vy
動かしてみると、いい感じに慣性が働いています。ゴムひもでつながった感じでしょうか。 最後には自機の場所に落ち着きますが、それまでは2秒に1回振動していますね。周波数で言えば、0.5Hzで振動しています。
「ばねダンパのパラメータ」を変えてみると、動き方を変えることができます。 できれば振動せずに自機の位置に止まってほしいです。サンプルでは減衰を1.0にするといい感じになりますが、毎回調整するとなると難しいですね。調整する目安が欲しいところです。 調べてみるとこんなサイトを見つけました。ありがたい。
技術レポート 減衰特性をあらわす係数 - ONOSOKKI
https://www.onosokki.co.jp/HP-WK/c_support/newreport/dampingfactor/dampingfactor_2.htm
どうやら設定したパラメータからいろいろとわかるようです。 振動する周波数の場合なら、まず振動角周波数ωを求めて、振動周波数に換算すると単位時間あたり何回振動するかが分かります。
ω = √(K/m)
ω = 2πf
という式なので、こうします。
w = sqrt(prmK / prmMass)
freq = w / (2.0 * M_PI) * 60.0
ここでの単位時間はフレームなので、最後に60フレームをかけて単位時間を秒にしています。
freqの単位はHzで、1秒あたりの振動する回数です。動かしてみると実際の動きとあっているようです。
他にも限界減衰率 Cc という値があり、減衰 C をこの値にすると振動せずに自機の座標の収まる動きをするようです。 また減衰を限界減衰率より大きくすると、自機に近づきにくくなるようです。便利そうな値なので求めて使ってみます。
cc = 2.0 * sqrt( prmMass * prmK)
prmD = cc
振動せずに、自機の位置にたどり着きました。これは便利。 最適な減衰は 1.047 だったようです。この値を手探りで見つけるのは難しいと思います。
さらに読んでみると、減衰比 ζ(ツェータ)を求めると振動具合の目安になるようです。
ζ = C / Cc なので、実装も簡単です。
; ζ<1 : 振動しながら収束
; ζ=1 : 緩やかに収束(一番いい感じの値)
; ζ>1 : おおきいほど緩やかに収束
zeta = prmD / cc
目安になる値が算出できたので、調整は何とかなりそうです。 質量 m を固定して、振動数がこのぐらいで、ζ がこのぐらいになるようにと決めてしまえば減衰 c もばね定数 k も迷うことなく決めることができそうです。
進行方向の後ろを追尾
他にもアイデアないかなーと、最後にChatGPTにも相談してみました。 するとなぜか1つのアイデアしか提供してくれません。もっとほかにもあるやろがいと思うのですが、なぜか1つのアイデアのみ提供してきます。聞き方が悪かったんでしょうか。 仕方がないので、紹介しておきます。
サンプルです。
; 自機の少し後ろを目標にして、自機を追いかけます。
;
sx = 0.0
sy = 0.0
v0 = 5.0
*main
redraw 1 : await 16 : redraw 0 : color 255, 255, 255 : boxf : color : pos 0,0
; 自機の前回座標
mx0 = mx
my0 = my
; 自機座標
mx = double(mousex)
my = double(mousey)
; 自機の移動速度
vmx = mx - mx0
vmy = my - my0
; ------------------------------
; 追跡座標
; ------------------------------
; 追跡目標座標
; 自機の進行方向の反対方向を追尾目標にしています。
lm = sqrt( vmx * vmx + vmy * vmy )
if lm = 0.0 {
tx = mx
ty = my
} else {
tx = mx - vmx / lm * 50.0
ty = my - vmy / lm * 50.0
}
; 追尾目標方向
lx = tx - sx
ly = ty - sy
l = sqrt(lx * lx + ly * ly) ; 距離
if l > 0.0 { ; ゼロ除算対策
; 移動速度より距離が近いと目標点を通り過ぎてしまいます。
; 通り過ぎて戻ろうとする動きを永遠に続けてしまいます。
; ここでの対策として、1フレーム後に目標点にぴったり一致する速度にしています。
v = v0
if l < v : v = l
; 方向ベクトル / 距離 で、方向単位ベクトルを算出。
; これを速度倍して、移動する方向と速度を算出。
vx = lx / l * v
vy = ly / l * v
; 移動後座標
; ここでの速度の単位の定義は、[ドット/フレーム]です。
; 次の座標=現在座標+速度×時間
; 時間:経過フレーム数。1フレームなので省略。
sx += vx
sy += vy
}
; ------------------------------
; 描画
; ------------------------------
; 自機
r = 5
color 0, 0, 255
circle mx-r, my-r, mx+r, my+r
; 追尾
color 255, 0, 0
circle sx-r, sy-r, sx+r, sy+r
color
line mx, my, sx, sy
; 目標点
color 255,0,0
line tx-r, ty, tx+r, ty
line tx, ty-r, tx, ty+r
goto *main
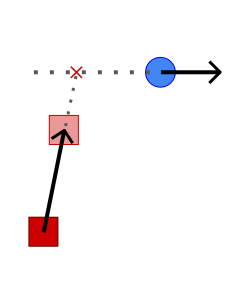
ChatGPTは、追跡の目標点を自機ではなく、自機の進行方向後ろ側にしろと言っています。 マウス操作なので自機の進行方向は、前回位置との差を使うことにします。
; 自機の前回座標
mx0 = mx
my0 = my
; 自機座標
mx = double(mousex)
my = double(mousey)
; 自機の移動速度
vmx = mx - mx0
vmy = my - my0
追跡目標を自機ではなく、移動方向の反対側にします。距離は適当に50にします。
; 追跡目標座標
; 自機の進行方向の反対方向を追尾目標にしています。
lm = sqrt( vmx * vmx + vmy * vmy )
if lm = 0.0 {
tx = mx
ty = my
} else {
tx = mx - vmx / lm * 50.0
ty = my - vmy / lm * 50.0
}
あとは、最初に紹介した追尾で追いかけます。
最短距離で追いかけようとせず、ちゃんと自機の後ろを追いかけてくれます。 しかし、自機の自動速度がマウスのため安定していないので目標点がぶれています。 自機との距離が近くなりすぎると、この影響が大きくなり動きが乱れます。 速度と方向が安定していればいいアイデアなんですが、マウスとの相性悪かったようです。
とはいえ追跡側の目標点を動かすというのは、いい着眼点です。ということで、流れ的に次は目標点を変更する話に入っていきます。
足跡
追跡側には自機が通った通りのルートを忠実に追いかけてほしい、というのが理想です。 ならば追跡側には、自機ではなく足跡をたどってもらうことにします。 そのためには、足跡を記録する必要があるので、その実装をやってみましょう。
; 自機が移動した足跡をと表示します。
; 一定時間(一定フレーム数)経過すると、足跡は消滅します。
;
logCnt = 30 ; 継続時間
dim logPx, logCnt
dim logPy, logCnt
logIdx = 0
*main
redraw 1 : await 16 : redraw 0 : color 255, 255, 255 : boxf : color : pos 0,0
; 自機座標
mx = mousex
my = mousey
; ------------------------------
; 足跡
; ------------------------------
; 足跡座標は、循環バッファに書き込みます。
; 書き込み開始位置を移動
logIdx++
if logIdx >= logCnt : logIdx = 0
; 足跡を書き込み
logPx(logIdx) = mx
logPy(logIdx) = my
; ------------------------------
; 描画
; ------------------------------
; 自機
r = 5
color 0, 0, 255
circle mx-r, my-r, mx+r, my+r
; 足跡
; 新しいデータら順に全てプロット
; バッファからFIFOで取り出す。
r = 2
idx = logIdx
x = logPx(idx)
y = logPy(idx)
repeat logCnt
x0 = x ; lineで描画するために1個前を記録
y0 = y
x = logPx(idx)
y = logPy(idx)
idx--
if idx < 0 : idx = logCnt - 1
color 255, 0, 0
circle x-r, y-r, x+r, y+r
color
line x0, y0, x, y
loop
goto *main
自機が移動した座標を全て足跡として記録してしまうとメモリがいくらあっても足りません。 それにそんなに長く記録をとる必要もないので、循環バッファ(リングバッファ)の中に足跡を記録します。 使用した変数は、次の通り。
- logCnt:足跡を記録する個数
- logPx, logPy:足跡の座標データ
- logIdx:足跡を配列に書き込む先頭位置
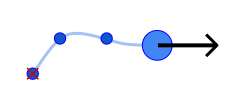
あとは足跡を描画する機能を付ければ完成です。 一番古い足跡を追跡目標にすれば、ほぼ正確に自機と同じルートを通って追いかけてくるようになるはずです。
実際作って動かしてみると、自機と同じ軌道をとりつつ、移動速度まで完全再現するほど完全に同じ動きを再現できます。 自機が止まって待っていると、追尾側は自機と同じ座標にまで追いつくことができます。
パンくず
足跡は、一定時間が経過すると消えてしまいます。自機が移動をやめると、全ての足跡が現在位置になってしまいます。 自機からは一定距離を保ちながら追いかけてほしいので、これでは困ります。 足跡は時間ではなく、距離とかで消えてくれたらいいのに。
というわけで、寿命が時間に依存しない足跡を考えてみました。 自機は一定距離進むごとに、通過点に印を残します。印の寿命は、フィールド上に存在できる個数で決めます。 距離依存にはなっていませんが、まあ大丈夫。 なお、ここでは印の事を童話「ヘンゼルとグレーテル」にちなんで「パンくず」と呼ぶことにしました。
ということで、サンプル。
; 自機が移動した足跡を表示します。
; 一定の距離以上移動しないと足跡は追加されません。
; 足跡の個数が一定上になると、古い足跡から消えます。
;
breadCnt = 30 ; 保持する個数
breadStep = 10 ; 足跡を残す距離
dim breadPx, breadCnt
dim breadPy, breadCnt
breadIdx = 0
*main
redraw 1 : await 16 : redraw 0 : color 255, 255, 255 : boxf : color : pos 0,0
; 自機座標
mx = mousex
my = mousey
; ------------------------------
; 足跡
; ------------------------------
; 足跡座標は、循環バッファに書き込みます。
; 書き込み開始位置を移動
; 前回の足跡からの距離が一定以上離れたら、新しい足跡を追記します。
; 最後の記録位置からの距離を確認
x = mx - breadPx(breadIdx)
y = my - breadPy(breadIdx)
if sqrt(x*x + y*y) > breadStep {
; 次の記録位置
breadIdx++
if breadIdx >= breadCnt : breadIdx = 0
; 足跡を書き込み
breadPx(breadIdx) = mx
breadPy(breadIdx) = my
}
; ------------------------------
; 描画
; ------------------------------
; 自機
r = 5
color 0, 0, 255
circle mx-r, my-r, mx+r, my+r
; 足跡
; 新しいデータら順に全てプロット
; バッファからFIFOで取り出す。
r = 2
idx = breadIdx
x = breadPx(idx)
y = breadPy(idx)
repeat breadCnt
x0 = x ; lineで描画するために1個前を記録
y0 = y
x = breadPx(idx)
y = breadPy(idx)
idx--
if idx < 0 : idx = breadCnt - 1
color 255, 0, 0
circle x-r, y-r, x+r, y+r
color
line x0, y0, x, y ; 足跡の軌跡
loop
goto *main
パンくずを記録する際は、最後のパンくずから現在位置までの距離を確認します。 一定距離(breadStep)離れていれば、記録に残すという要領です。 循環バッファに記録する点は、足跡と同じです。
; 最後の記録位置からの距離を確認
x = mx - breadPx(breadIdx)
y = my - breadPy(breadIdx)
if sqrt(x*x + y*y) > breadStep {
; 次の記録位置
breadIdx++
if breadIdx >= breadCnt : breadIdx = 0
; 足跡を書き込み
breadPx(breadIdx) = mx
breadPy(breadIdx) = my
}
一番古い足跡を追跡目標にすれば、ほぼ正確に自機と同じルートを通って追いかけてくるようになるはずです。 自機が移動をやめても消えないし、常にある程度以上の距離を保ち続けてくれます。かなり理想に近づいた気がしますね。
パンくずと追尾
では、パンくずを追尾させてみましょう。
; 自機が移動した一番古い足跡を目標にして追尾します。
;
; 追いかけるキャラクター
sx = 0.0
sy = 0.0
v0 = 5.0
; 足跡
breadCnt = 3 ; 保持する個数
breadStep = 20 ; 足跡を残す距離
dim breadPx, breadCnt
dim breadPy, breadCnt
breadIdx = 0
*main
redraw 1 : await 16 : redraw 0 : color 255, 255, 255 : boxf : color : pos 0,0
; 自機座標
mx = mousex
my = mousey
; ------------------------------
; 足跡
; ------------------------------
; 足跡座標は、循環バッファに書き込みます。
; 書き込み開始位置を移動
; 前回の足跡からの距離が一定以上離れたら、新しい足跡を追記します。
x = mx - breadPx(breadIdx)
y = my - breadPy(breadIdx)
if sqrt(x*x + y*y) > breadStep {
breadIdx++
if breadIdx >= breadCnt : breadIdx = 0
; 足跡を書き込み
breadPx(breadIdx) = mx
breadPy(breadIdx) = my
}
; ------------------------------
; 一番古い足跡
; ------------------------------
; 追尾目標座標
; 自機の一番古い足跡を目標に追いかけます。
idx = breadIdx + 1
if idx >= breadCnt : idx = 0
tx = breadPx(idx)
ty = breadPy(idx)
; ------------------------------
; 追尾
; ------------------------------
; 追尾目標方向
lx = double(tx) - sx
ly = double(ty) - sy
l = sqrt(lx * lx + ly * ly) ; 距離
if l > 0.0 { ; ゼロ除算対策
; 速度
v = v0
if l < v : v = l ; 速度制限
; 移動ベクトル
vx = lx / l * v
vy = ly / l * v
; 移動後座標
sx += vx
sy += vy
}
; ------------------------------
; 描画
; ------------------------------
; 自機
r = 5
color 0, 0, 255
circle mx-r, my-r, mx+r, my+r
; 足跡
; 一番古い足跡
r = 2
color 0, 0, 0
circle tx-r, ty-r, tx+r, ty+r
; 追尾
r = 5
color 255, 0, 0
circle sx-r, sy-r, sx+r, sy+r
; 足跡の奇跡を描画
; 新しいデータから順に全てプロット
; バッファからFIFOで取り出す。
color 128,128,128
idx = breadIdx
x = breadPx(idx)
y = breadPy(idx)
repeat breadCnt
x0 = x ; lineで描画するために1個前を記録
y0 = y
x = breadPx(idx)
y = breadPy(idx)
idx--
if idx < 0 : idx = breadCnt - 1
line x0, y0, x, y
loop
goto *main
ゆっくり動くと、追尾側の動きがカクカクになります。 離れた瞬間に全力で追いかけるし、パンくずが消えるのも一定の時間間隔ではないので仕方がありません。
追跡側が目標点に追いつく直前の速度をちょっと工夫してみます。
if l < v : v = l ; 速度制限
この行をこうします。
;if l < v : v = l ; 速度制限
if l < 40.0 { ; 減速
v *= l / 40.0
}40.0は、減速開始距離です。 追いかける側と目標点までの距離が、この値より近くなったら減速します。 パンくずを置く距離間隔より大きい値を指定します。ここでは2倍を指定してみました。
これで動きが少し滑らかになりました。
モジュールにする
いい感じになってきたような気がします。 もう少しいろいろ触って感触を確かめないと、使い物になるか判断が付きにくいのでモジュールにしてみます。
; 追跡モジュール
#module
;///////////////////////////////////////////////////////////////////////////////////////////////////
;
; 牽引された子座標を取得
;
;[ Infomation ]
; GetPullChildPos childPosX1, childPosY1, childPosX0, childPosY0, armLength, parentPosX1, parentPosY1
; var childPosX1 : [OUT] 移動後の子座標 X
; var childPosY1 : [OUT] 移動後の子座標 Y
; double childPosX0 : [IN] 移動前の子座標 X
; double childPosY0 : [IN] 移動前の子座標 Y
; double armLength : [IN] 親と子を連結する距離
; double parentPosX1 : [IN] 移動後の親座標 X
; double parentPosY1 : [IN] 移動後の親座標 Y
;
;
;[ comment ]
;
#deffunc GetPullChildPos var childPosX1, var childPosY1, double childPosX0, double childPosY0, double armLength, double parentPosX1, double parentPosY1
; 距離
x = childPosX0 - parentPosX1
y = childPosY0 - parentPosY1
l = sqrt(x * x + y * y)
; 牽引されている点の座標を計算
; if l > armLength { ; 紐
if l ! 0 { ; 固い梁
; ターゲット(mx,my)から既定の長さ距離の位置に移動
childPosX1 = x / l * armLength + parentPosX1
childPosY1 = y / l * armLength + parentPosY1
} else {
childPosX1 = childPosX0
childPosY1 = childPosY0
}
return
;///////////////////////////////////////////////////////////////////////////////////////////////////
;
; 紐で牽引された子座標を取得
;
;[ Infomation ]
; GetStringPullChildPos childPosX1, childPosY1, childPosX0, childPosY0, armLength, parentPosX1, parentPosY1
; var childPosX1 : [OUT] 移動後の子座標 X
; var childPosY1 : [OUT] 移動後の子座標 Y
; double childPosX0 : [IN] 移動前の子座標 X
; double childPosY0 : [IN] 移動前の子座標 Y
; double armLength : [IN] 親と子を連結する距離
; double parentPosX1 : [IN] 移動後の親座標 X
; double parentPosY1 : [IN] 移動後の親座標 Y
;
;
;[ comment ]
;
#deffunc GetStringPullChildPos var childPosX1, var childPosY1, double childPosX0, double childPosY0, double armLength, double parentPosX1, double parentPosY1
; 距離
x = childPosX0 - parentPosX1
y = childPosY0 - parentPosY1
l = sqrt(x * x + y * y)
; 牽引されている点の座標を計算
if l > armLength { ; 紐
; if l ! 0 { ; 固い梁
; ターゲット(mx,my)から既定の長さ距離の位置に移動
childPosX1 = x / l * armLength + parentPosX1
childPosY1 = y / l * armLength + parentPosY1
} else {
childPosX1 = childPosX0
childPosY1 = childPosY0
}
return
; ------------------------------------------------------------------------------
; 追尾
; v_vx, v_vy : [OUT] 移動速度
; p_myx, p_myx : 移動前の座標
; p_tx, p_ty : 追尾目標座標
; p_vel : 移動速度
#deffunc tuibi var v_vx, var v_vy, double p_myx, double p_myy, double p_tx, double p_ty, double p_vel
v_vx = 0.0
v_vy = 0.0
; 追尾目標方向
lx = p_tx - p_myx
ly = p_ty - p_myy
l = sqrt(lx * lx + ly * ly) ; 距離
if l > 0.0 { ; ゼロ除算対策
; 移動速度より距離が近いと目標点を通り過ぎてしまいます。
; 通り過ぎて戻ろうとする動きを永遠に続けてしまいます。
; ここでの対策として、1フレーム後に目標点にぴったり一致する速度にしています。
v = p_vel
if l < v : v = l
; 方向ベクトル / 距離 で、方向単位ベクトルを算出。
; これを速度倍して、移動する方向と速度を算出。
v_vx = lx / l * v
v_vy = ly / l * v
}
return
; ------------------------------------------------------------------------------
; 追尾して減速
; v_vx, v_vy : [OUT] 移動速度
; p_myx, p_myx : 移動前の座標
; p_tx, p_ty : 追尾目標座標
; p_vel : 移動速度
; p_length : 減速開始距離
#deffunc tuibi_s var v_vx, var v_vy, double p_myx, double p_myy, double p_tx, double p_ty, double p_vel, double p_length
v_vx = 0.0
v_vy = 0.0
; 追尾目標方向
lx = p_tx - p_myx
ly = p_ty - p_myy
l = sqrt(lx * lx + ly * ly) ; 距離
if l > 0.0 { ; ゼロ除算対策
; 移動速度より距離が近いと目標点を通り過ぎてしまいます。
; 通り過ぎて戻ろうとする動きを永遠に続けてしまいます。
; ここでの対策として、1フレーム後に目標点にぴったり一致する速度にしています。
v = p_vel
if l < p_length { ; 減速
v *= l / p_length
}
; 方向ベクトル / 距離 で、方向単位ベクトルを算出。
; これを速度倍して、移動する方向と速度を算出。
v_vx = lx / l * v
v_vy = ly / l * v
}
return
; ------------------------------------------------------------------------------
; ばねダンパ
; Spring damper system
; v_vx, v_vy : [OUT] 移動速度
; p_myx, p_myx : 移動前の座標
; p_tx, p_ty : 追尾目標座標
; p_vx, p_vy : 現在の移動速度
;
; zeta,w,freqは、意味がないので消しても大丈夫です。
#deffunc springD var v_vx, var v_vy, double p_myx, double p_myy, double p_tx, double p_ty, double p_vx, double p_vy
; ばねダンパのパラメータ
prmK = 0.02741 ; ばね定数
prmD = 0.5 ; 減衰
prmMass = 2.0 ; 質量
; 限界減衰率
; 減衰をこの値より小さくすると、振動しながら収束するようになります。
; 減衰をこの値より大きくすると、振動せずに収束しますが、大きすぎるとなかなか目標点に到達できません。
cc = 2.0 * sqrt( prmMass * prmK)
prmD = cc ; 振動しない
;prmD = cc*0.6 ; 少し振動
; 減衰比
; この値を調べることで、振動がどのような挙動で減衰していくかが分かります。
; <1 : 振動しながら収束
; =1 : 緩やかに収束(一番いい感じの値)
; >1 : おおきいほど緩やかに収束
zeta = prmD / cc
; 振動角周波数
; 振動周波数を求めるための途中経過の値です。
; ω = √(K/m)
w = sqrt(prmK / prmMass)
; 振動周波数
; 1秒間に何回振動するかを示す値です。次式から求めます。
; ω = 2πf
; 出てくる値は、フレームあたりの回数なので、1秒あたりに変換
freq = w / (2.0 * M_PI) * 60.0
; 変化後速度
v_vx = 0.0
v_vy = 0.0
; 追尾目標方向
lx = p_myx - p_tx
ly = p_myy - p_ty
l = sqrt(lx * lx + ly * ly) ; 距離
if l > 0.1 { ; 無限振動対策
; 距離が近くなると振動がなかなか収まらないので、
; 一定距離まで近づいたら、計算しないようにしています。
; ばね・ダンパ
; 方向ごとに速度を計算します。
; 前回速度
vx0 = p_vx
vy0 = p_vy
; 力
fx = - prmK * lx - prmD * vx0
fy = - prmK * ly - prmD * vy0
; 速度=加速度+前回速度
v_vx = fx / prmMass + vx0
v_vy = fy / prmMass + vy0
}
return
#global
では、モジュールを使って適当なサンプルを書いてみます。 ついでに動作比較がしやすいように、紹介した各機能を切り替えて動かせるようにしてみます。
; ------------------------------
; 動作設定
; ------------------------------
; 目標点の種類指定
typeTgt = "親"
;typeTgt = "後ろに回り込み"
;typeTgt = "一番古いパンくず"
; 追跡
;typeTrac = "追尾"
;typeTrac = "追尾後に減速"
typeTrac = "ばねダンパ"
;typeTrac = "紐" ; typeTgtは、無視します。
;typeTrac = "棒" ; typeTgtは、無視します。
; ------------------------------
; 変数初期化
; ------------------------------
; 足跡の全ログ
logCnt = 60 ; 保持する個数
ddim logPx, logCnt
ddim logPy, logCnt
logIdx = 0
; パンくず
breadCnt = 5 ; 保持する個数
breadStep = 20 ; 足跡を残す距離
ddim breadPx, breadCnt
ddim breadPy, breadCnt
breadIdx = 0
; 追跡する側
sx = 0.0 ; 座標
sy = 0.0
v0 = 5.0 ; 速度
; ------------------------------
; メインループ
; ------------------------------
*main
redraw 1 : await 16 : redraw 0 : color 255, 255, 255 : boxf : color : pos 0,0
; 親座標
mx0 = mx
my0 = my
mx = double(mousex)
my = double(mousey)
; ------------------------------
; 足跡
; ------------------------------
; 親が移動した座標をすべて記録します。
; 足跡座標は、循環バッファに書き込みます。
; 書き込み開始位置を移動
logIdx++
if logIdx >= logCnt : logIdx = 0
; 足跡を書き込み
logPx(logIdx) = mx
logPy(logIdx) = my
; ------------------------------
; パンくず
; ------------------------------
; 追跡側が通過した座標から、一定距離置きに記録を行います。
; 前回の足跡からの距離が一定以上離れたら、新しい足跡を追記します。
; パンくず座標は、循環バッファに書き込みます。
x = mx - breadPx(breadIdx)
y = my - breadPy(breadIdx)
if sqrt(x*x + y*y) > breadStep {
breadIdx++
if breadIdx >= breadCnt : breadIdx = 0
; 足跡を書き込み
breadPx(breadIdx) = mx
breadPy(breadIdx) = my
}
; ------------------------------
; 目標点
; ------------------------------
; 親
if typeTgt = "親" {
tx = mx
ty = my
}
; 後ろに回り込み
if typeTgt = "後ろに回り込み" {
; 親の移動速度
vmx = mx - mx0
vmy = my - my0
lm = sqrt( vmx * vmx + vmy * vmy )
if lm = 0.0 {
tx = mx
ty = my
} else {
tx = mx - vmx / lm * 50.0
ty = my - vmy / lm * 50.0
}
}
; 一番古いパンくず
if typeTgt = "一番古いパンくず" {
idx = breadIdx + 1
if idx >= breadCnt : idx = 0
tx = breadPx(idx)
ty = breadPy(idx)
}
; ------------------------------
; 追跡
; ------------------------------
; 追尾
if typeTrac = "追尾" {
tuibi vx, vy, sx, sy, tx, ty, v0
}
; 追尾後に減速
if typeTrac = "追尾後に減速" {
tuibi_s vx, vy, sx, sy, tx, ty, v0, 40
}
; ばねダンパ
if typeTrac = "ばねダンパ" {
springD vx, vy, sx, sy, tx, ty, vx, vy
}
; 紐で引っ張る
if typeTrac = "紐" {
tx = mx ; 目標座標は固定
ty = my
GetStringPullChildPos x, y, sx, sy, 50, tx, ty
vx = x - sx
vy = y - sy
}
; 棒で連結
if typeTrac = "棒" {
tx = mx ; 目標座標は固定
ty = my
GetPullChildPos x, y, sx, sy, 50, tx, ty
vx = x - sx
vy = y - sy
}
; 移動後座標
sx += vx
sy += vy
; ------------------------------
; 描画
; ------------------------------
; 親軌跡
; ログに残っている全ての足跡を描画します。
idx = logIdx
x = logPx(idx)
y = logPy(idx)
color 200, 200, 255
repeat logCnt
x0 = x ; lineで描画するために1個前を記録
y0 = y
x = logPx(idx)
y = logPy(idx)
idx--
if idx < 0 : idx = logCnt - 1
line x0, y0, x, y
loop
; パンくず
; 新しいデータら順に全てプロット
; バッファからFIFOで取り出す。
r = 2
idx = breadIdx
x = breadPx(idx)
y = breadPy(idx)
color 128, 128, 255
repeat breadCnt
x0 = x ; lineで描画するために1個前を記録
y0 = y
x = breadPx(idx)
y = breadPy(idx)
idx--
if idx < 0 : idx = breadCnt - 1
circle x-r, y-r, x+r, y+r
line x0, y0, x, y ; 足跡の軌跡
loop
; 親
r = 5
color 0, 0, 255
circle mx-r, my-r, mx+r, my+r
; 追尾
color 255, 0, 0
circle sx-r, sy-r, sx+r, sy+r
; 追尾目標点
color 255, 0, 0
line tx-r, ty , tx+r, ty
line tx , ty-r, tx , ty+r
color
line mx, my, sx, sy
goto *main
動作設定の所のコメント箇所を変えれば、各機能を切り替えできます。 追跡の目標点と追跡方法を選べます。組み合わせを変えて遊んでみてください。 予想外にも「後ろに回り込み」と「ばねダンパ」にすると、自機の軌道に近い動きを見せてくれるようです。
数珠繋ぎにしてみる
試してはみたものの、違いがあまりないような気もします。 そこで、追跡側を数珠つなぎにしてみることにしました。 数珠つなぎにするので、呼び名も変更します。「親→親node」「追跡側→追跡node」
さっきのモジュールを使ったサンプルです。
; ------------------------------
; 動作設定
; ------------------------------
; 目標点の種類指定
typeTgt = "親"
;typeTgt = "後ろに回り込み"
;typeTgt = "一番古いパンくず"
; 追跡
;typeTrac = "追尾"
;typeTrac = "追尾後に減速"
typeTrac = "ばねダンパ"
;typeTrac = "紐" ; typeTgtは、無視します。
;typeTrac = "棒" ; typeTgtは、無視します。
; ------------------------------
; 変数初期化
; ------------------------------
; 足跡の全ログ
logCnt = 60 ; 保持する個数
ddim logPx, logCnt
ddim logPy, logCnt
logIdx = 0
; 追跡する側
nodeCnt = 15 ; 個数
ddim nx0, nodeCnt ; 前ループ座標
ddim ny0, nodeCnt
ddim nx, nodeCnt ; 座標
ddim ny, nodeCnt
ddim nvx, nodeCnt ; 速度
ddim nvy, nodeCnt
; 初期位置
repeat nodeCnt
nx(cnt) = double(rnd(ginfo_winx))
ny(cnt) = double(rnd(ginfo_winy))
loop
; パンくず
breadCnt = 5 ; 保持する個数
breadStep = 20 ; 足跡を残す距離
ddim breadPx, nodeCnt, breadCnt
ddim breadPy, nodeCnt, breadCnt
dim breadIdx, nodeCnt
sx = 0.0 ; 座標
sy = 0.0
v0 = 5.0 ; 速度
; ------------------------------
; メインループ
; ------------------------------
*main
redraw 1 : await 16 : redraw 0 : color 255, 255, 255 : boxf : color : pos 0,0
; 親node座標
mx0 = mx
my0 = my
mx = double(mousex)
my = double(mousey)
; 前ループの座標を保存
repeat nodeCnt
nx0(cnt) = nx(cnt)
ny0(cnt) = ny(cnt)
loop
; 追跡ノードの座標を更新
nx(0) = mx
ny(0) = my
; ------------------------------
; 足跡
; ------------------------------
; 親nodeが移動した座標をすべて記録します。
; 足跡座標は、循環バッファに書き込みます。
; 書き込み開始位置を移動
logIdx++
if logIdx >= logCnt : logIdx = 0
; 足跡を書き込み
logPx(logIdx) = mx
logPy(logIdx) = my
; ------------------------------
; パンくず
; ------------------------------
; 追跡nodeが通過した座標から、一定距離置きに記録を行います。
; 前回の足跡からの距離が一定以上離れたら、新しい足跡を追記します。
; パンくず座標は、循環バッファに書き込みます。
; 書き込み開始位置を移動
repeat nodeCnt
x = nx(cnt) - breadPx(cnt, breadIdx(cnt))
y = ny(cnt) - breadPy(cnt, breadIdx(cnt))
if sqrt(x*x + y*y) > breadStep {
breadIdx(cnt)++
if breadIdx(cnt) >= breadCnt : breadIdx(cnt) = 0
; 足跡を書き込み
breadPx(cnt, breadIdx(cnt)) = nx(cnt)
breadPy(cnt, breadIdx(cnt)) = ny(cnt)
}
loop
; ------------------------------
; 追跡軌道を計算
; ------------------------------
; 1つ目は座標が決まっているので、2つ目から座標を計算。
repeat nodeCnt - 1, 1
sx = nx(cnt)
sy = ny(cnt)
vx = nvx(cnt)
vy = nvy(cnt)
; ------------------------------
; 目標点
; ------------------------------
; 親node
if typeTgt = "親" {
tx = nx(cnt-1)
ty = ny(cnt-1)
}
; 後ろに回り込み
if typeTgt = "後ろに回り込み" {
tx = nx(cnt-1) - (nx(cnt-1) - nx0(cnt-1)) * 5.0
ty = ny(cnt-1) - (ny(cnt-1) - ny0(cnt-1)) * 5.0
}
; 一番古いパンくず
if typeTgt = "一番古いパンくず" {
idx = breadIdx(cnt-1) + 1
if idx >= breadCnt : idx = 0
tx = breadPx(cnt-1, idx)
ty = breadPy(cnt-1, idx)
}
; ------------------------------
; 追跡
; ------------------------------
; 追尾
if typeTrac = "追尾" {
tuibi vx, vy, sx, sy, tx, ty, v0
}
; 追尾後に減速
if typeTrac = "追尾後に減速" {
tuibi_s vx, vy, sx, sy, tx, ty, v0, 40
}
; ばねダンパ
if typeTrac = "ばねダンパ" {
springD vx, vy, sx, sy, tx, ty, vx, vy
}
; 紐で引っ張る
if typeTrac = "紐" {
tx = nx(cnt-1) ; 目標座標は固定
ty = ny(cnt-1)
GetStringPullChildPos x, y, sx, sy, 30, tx, ty
vx = x - sx
vy = y - sy
}
; 棒で連結
if typeTrac = "棒" {
tx = nx(cnt-1) ; 目標座標は固定
ty = ny(cnt-1)
GetPullChildPos x, y, sx, sy, 30, tx, ty
vx = x - sx
vy = y - sy
}
; 移動後座標
sx += vx
sy += vy
nx(cnt) = sx
ny(cnt) = sy
nvx(cnt) = vx
nvy(cnt) = vy
loop
; ------------------------------
; 描画
; ------------------------------
; 親node軌跡
; ログに残っている全ての足跡を描画します。
idx = logIdx
x = logPx(idx)
y = logPy(idx)
color 200, 200, 255
repeat logCnt
x0 = x ; lineで描画するために1個前を記録
y0 = y
x = logPx(idx)
y = logPy(idx)
idx--
if idx < 0 : idx = logCnt - 1
line x0, y0, x, y
loop
; パンくず
; 新しいデータら順に全てプロット
; バッファからFIFOで取り出す。
if typeTgt = "一番古いパンくず" {
repeat nodeCnt
n = cnt
r = 2
idx = breadIdx(n)
x = breadPx(n, idx)
y = breadPy(n, idx)
color 128, 128, 255
repeat breadCnt
x0 = x ; lineで描画するために1個前を記録
y0 = y
x = breadPx(n, idx)
y = breadPy(n, idx)
idx--
if idx < 0 : idx = breadCnt - 1
circle x-r, y-r, x+r, y+r
line x0, y0, x, y ; 足跡の軌跡
loop
loop
}
; 連結部分
; 追尾nodeを連結した直線を描画。
color 128,128,128
pos nx(0), ny(0)
repeat nodeCnt - 1, 1
line nx(cnt), ny(cnt)
loop
; 親node
r = 10
color 0, 0, 255
circle mx-r, my-r, mx+r, my+r
; 追尾node
r = 5
repeat nodeCnt
c = cnt * 240 / nodeCnt
color 255, c, c
sx = nx(cnt)
sy = ny(cnt)
circle sx-r, sy-r, sx+r, sy+r
loop
goto *main
動作設定の所のコメント箇所を変えれば、各機能を切り替えできます。 少し動きに違いが出てきましたね。
目標点を「後ろに回り込み」にしたり「パンくず」にすると、比較的上手く親が通った後を追いかけてくれるようです。 完璧に親の足跡を追いかけてくれるものはありませんね。 追跡を紐か棒にするとけん引を使った方法になるのですが、これを選ぶと床上を紐や鎖をはわせたような動きになりました。 速度などのパラメータを変更してみると、また動きに変化が現れます。
まとめ
いろいろ試したので、傾向を整理してみます。
基本的に親nodeの速度が追跡nodeよりも遅い場合、追跡nodeは親nodeの軌道に近い場所を通る傾向があります。 逆に親nodeの速度が速いほど、追跡nodeは内側の軌道を通る傾向があります。 ただし、進行方向の後ろに回り込む方法の場合だけは、調整次第で追跡nodeがカーブの外側を通る場合があります。 また「追尾後に減速」する方法は、追跡node間でも同じ軌道の維持をする能力が低いようです。 表にまとめてみました。
○:親の軌道と近い軌道を移動できる。
△:追跡nodeどうしは同じ軌道を通る。
×:同じ軌道を通らない。
| 目標点 | 追跡方法 | 遅い | 速い | 傾向 |
|---|---|---|---|---|
| 親 | 追尾 | - | × | 追尾nodeが1か所に集まってしまう。とにかくダメ。 |
| 親 | 追尾後に減速 | × | × | ばねダンパとあまり変わらない。 |
| 親 | ばねダンパ | × | × | 追尾後に減速とあまり変わらない。 |
| 後ろに回り込み | 追尾 | ○ | △ | カーブの際に外側の軌道を通ることがある。調整は難しい。 |
| 後ろに回り込み | 追尾後に減速 | × | × | 軌道は改善されるが、同じ軌道を通らない。 |
| 後ろに回り込み | ばねダンパ | ○ | ○ | ばね係数を大きくすると、同じ軌道に乗りやすい。 |
| 一番古いパンくず | 追尾 | ○ | △ | 追跡nodeの動きがカクカクになる。親nodeの速度が速くても、追跡node間の軌道再現度は高い。 |
| 一番古いパンくず | 追尾後に減速 | × | × | 速度が遅いと追跡nodeの動きがぎこちなくなる。 |
| 一番古いパンくず | ばねダンパ | × | × | 速度が遅いと追跡nodeの動きがぎこちなくなる。 |
| 親 | 紐・棒 | × | × | node間の距離を一定に保てる。他の方法に比べ、速度を上げても軌道の変化が小さい。棒は、引き返した際の動作が特殊。 |
親nodeの進行方向の後ろに目標点を置いて、ばねダンパで結合するのがこの中では最も求めていた動きに近い動作をするようです。 循環バッファに足跡を記録する必要もありませんし、ばねダンパは物理シミュレーションとの相性もいいので使い勝手がよさそうですね。 とはいえ、どれもそれぞれ特徴のある動きをするので、状況に合わせていい方法を選ぶのがよいかと思います。 シューティングゲームならどれ使っても面白そうですし。 そもそも速度やカーブの曲率などの運用条件によって、どの組み合わせのどんな設定がいいかというのも変わってくると思います。 状況と好みでお好きなものを。
もっと精度よく追跡するには、パンくずの寿命を追跡側が食べるまで、とすればもっと精度が上がりそうですが…実装が面倒くさそうなのであまりやりたくないな。 後は、昔作ったタイヤの前輪後輪の関係を再現したアルゴリズムで、数珠繋ぎを試してみたいところ。