はじめに

　先日実装したHSP3用モジュールの軌道予測関連命令 d2cShot_GetShotData 命令の解説をしてみます。 この命令は、等速直線運動している目標物に攻撃（これも等速直線運動）を当てるために必要な射出方向を計算します。 定数として与えるのは、目標の移動速度（X, Y）と現在位置（X, Y）、攻撃の射出位置（X, Y）と攻撃の射出速度です。

　計算結果として、攻撃の射出速度（X, Y）と衝突予想座標（X, Y）、衝突までの時間を返します。 攻撃を計算結果の射出速度で打ち出すと目標に衝突します。算出される射出速度の絶対値は、定数として与えた射出速度と同じ値です。

　置きエイムどころか攻撃そのものを目標の移動予定地点に置くような攻撃が可能になります。敵NPCに気軽に搭載してしまうとゲームバランスに影響しそうなので配慮が必要です。

位置と時間の表現

　基本的な考え方は、↓このサイトで解説しているものと同じような方針です。
その９　移動する２つの球の衝突場所と時刻を得る
http://marupeke296.com/COL_3D_No9_GetSphereColliTimeAndPos.html

　移動する物体 A, B を考えたとき、A, B間の距離を求めて、この距離がゼロになる時刻に A, B は衝突する。という方針です。 解説では物体 A,B の大きさを考慮して一定値以下になれば衝突としていますが、今回は物体の大きさを考慮せずに大きさを持たない A, B の軌道が交差する瞬間（点）を計算します。大きな違いはないですね。 大きな違いとしては、攻撃はまだ打ち出していないので速度しかわかっていません。

今回の図を書いてみました。

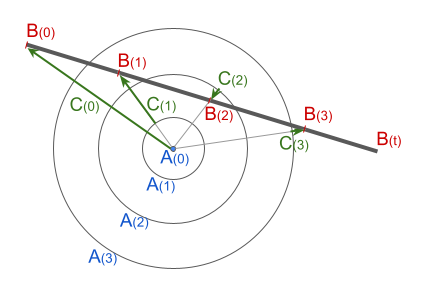
　A を攻撃、B を目標とします。 攻撃 A は速度しかわかっていないので時間経過ごとに進む距離だけを描いています。半径が一定速度で広がる絵です。多少ずれてますが目をつぶってください。 黒い太線が B の軌道です。これも一定速度で移動しています。 C （緑のベクトル）は A から B までの最短距離…というと語弊がありますが、図のような位置のベクトルです。

　ABCの右下のカッコは時刻を示します。ABCを時間の関数で表しています。 A(0)が攻撃の射出位置、A(1)が時刻 t=1 のときの A の移動距離です。 B(0)が目標の現在位置、B(1)が時刻 t=1 のときの B の位置です。

　Aを B(1) の方向に射出すると t=1 のときはまだ距離があります。このまま進んでも B の後ろを通過します。 B(2) の方向に射出すると A は B の軌道を通過しますが、Bよりも先を通過してしまいます。 Cの長さがゼロになる場所を狙えば、当たるということはなんとなく図からわかると思います。 また、Cの長さがゼロになる場所は、B(1)とB(2)の間、B(2)とB(3)の間にありそうということも図からなんとなく予想が付きますね。

　ところで、A(t)の正確な位置はまだわかっていないので、図の中には描いていません。 便宜上、A(t) が移動する距離を Ra(t) と書くことにします。図中の円の半径ですね。

　もう一つ計算の便宜上、攻撃の射出位置 A(0) から B(t) へのベクトルを D(t) とします。

数式に起こす

変数を決めて計算式に起こしてみます。

• A(t) : 時刻 t のときの A 座標ベクトル
• B(t) : 時刻 t のときの B 座標ベクトル
• C(t) : A(0)からB(t)までベクトルからAのt時点における到達可能距離を引いたベクトル
• D(t) : 時刻 t のときの A(0) から B(t) へのベクトル
• Ra(t) : 時刻 t のときの A の移動半径
• Va : Aの移動速度（一定速度）
• Vb : Bの移動速度（一定速度）

　Cの表現が難しいですね。なお、A,B,C,D はベクトル、Ra,Va,Vb はスカラーとします。 ある時刻 t におけるベクトルC（図の緑のベクトル）…つまりC(t)を

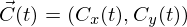
と表すことにします。A,B,Dも同様です。ベクトルなんで、長さを取るときは √(Cx(t)^2 + Cy(t)^2) などとやります。

では使うのは後の方ですが、わかりやすそうなところから書き出しておきます。

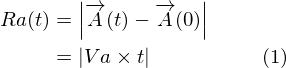
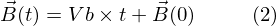
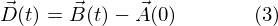
　言葉で書いたとおりです。さて A(t) は求めたい関数なのでわかりません。わかったら苦労しないのです。 ということで残りは C(t) です。 ベクトルD(t)からベクトルD(t)の長さをRa(t)にしたベクトルを引くと出てきます。

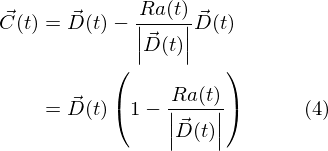
　必要なことが書き起こせたので、ここから衝突する条件を考えていきます。 ベクトルC(t)の長さがゼロになるとき、AとBは衝突します。 長さは2乗してルートを取れば出てきます。

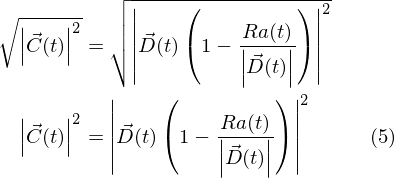
この式から、

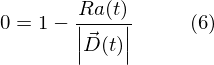
を満たす t を求めれば良さそうなことがわかります。 |D(t)|をゼロにするのはダメそうですね。無限大になっちゃうし。 あとはひたすらこの式を解いて t の式に整理していきます。

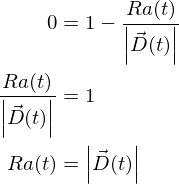
(1)より

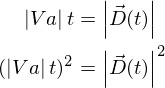
(3)より

(4)より

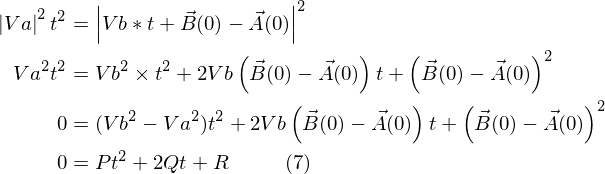
　P,Q,Rはそれぞれ、

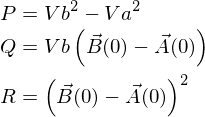
です。いずれも定数ですね。計算式も時刻 t の2次方程式になりました。なんとか解けそうです。 この時点で、解は1～2個、解無しの場合がありえることがわかります。図の場合は、解が2つありそうという予想にも一致しますね。

衝突時刻の算出

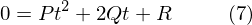
　P,Q,Rは定数なので、(7)式は時刻 t の2次方程式です。 これを解けばいいので、2次方程式の解の公式を用いて t を算出します。

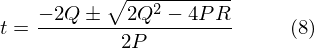
　算出された衝突時刻 t から衝突予想位置を求めます。B(t)の式に求めた t を入れれば出てきます。

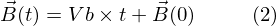
　未知数 t と算出した数値 t に同じ変数を使っちゃったから同じ式になってしまった…。すみません。

　Aを算出した衝突予想位置に向かって射出するための速度を算出します。方向は D(t) なので、

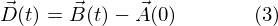
の長さを Va にします。

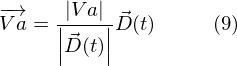
　これでようやく攻撃 A の射出速度（方向含む）が算出できました。この速度で打ち出せば当たる…はずなのですが、そうでもありません。もう少し掘り下げて見ていきます。

P,Q,Rの意味

　ここでP,Q,Rの意味について考えてみます。

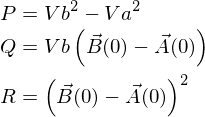
• P : A、Bの速度差の2乗
• Q : Bの速度 × 移動開始点の距離差
• R : 移動開始点の距離差の2乗

　だいたいこんな感じでしょうか。数式のまんまで申し訳ないです。数学に強い方ならもう少し意味が読み取れるかもしれませんね。 これを踏まえて次の例外を見ていきます。

例外

　どうしても数学上算出できない条件というものがあります。例えばゼロ割などです。そのような例外の意味と対策について考えてみます。

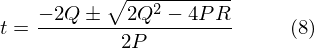
　2次方程式の解は、ルートの中がマイナスになる場合解がありません。つまり衝突しないということです。 4PR が正の値で 2Q^2 よりも大きいという場合です。 Rは必ず正なので、Pも正つまり

Vb ＞ Va　（∵Vb ≧ 0, Va ≧ 0）

　目標のほうが速度が早い条件ということになります。式からはこれ以上読み取るのは困難ですが、方向が悪くて目標に追いつけない状態です。

　また P = 0 の場合もゼロ割になるので計算できません。この場合は、1次方程式として解きます。 P = 0 は、速度が同じという意味なので、衝突する点は A(0) と B(0) を結んだ線分を2等分して直行する直線上にあります。(7)式より

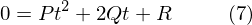
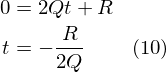
　さらに、この式では Q = 0 の場合は答えが出ません。 Bの速度がゼロか、A,Bの距離がゼロの場合です。より答えを求めるのは簡単なので省略します。

　また、これらの計算の結果 t ＜ 0 になることがあります。すでに時間が過ぎてしまった過去に衝突時刻があるということなので今回は解として使用できません。

まとめ

　数学的な求める手順としては、以上になります。プログラミングする上では他にも考える必要があることがあります。 出てきた答えが２つある場合は、より0に近い方を選択する。だとか…。 速度が同じはずなので P はゼロになるはずなのに、実数計算の僅かな誤差で P がゼロになってくれない。そのせいで衝突時刻がゼロという計算結果が出てしまう。 この場合は、再度１次方程式の方で解き直す。とかですね。

　さてこの計算をゲームに実装すると、アニメでよく見るような攻撃で攻撃を撃ち落とすとか、 アムロみたいなニュータイプっぽい攻撃とかができるようになるはずです。 来そうなところにバラ撒くでなく、置きエイムで待ち構えるでなく、移動先に１発だけ「攻撃を置く」ために射出する攻撃です。的に実装すると怖いですね。 一方で、ミサイル（速度や方向が変わる物）に当てるとかマリオみたいに加速度を受けてジャンプ/落下するものには当てることができません。

　このように実装すると大変楽しそうではありますが、注意や配慮も必要だと思います。 一定速度という条件下なので相手が攻撃を撃ったらすぐに方向を変えたり加減速すれば回避は簡単です。 動きを変えさせられるとも言い変えることができますね。 この辺を踏まえてゲームに実装しないとただのえげつない攻撃になるので注意が必要だと思います。