「影」とは

　まずはじめに、ここで扱う「影」は便宜上、影っぽいから「影」と呼んでいるだけで物理的に正しい影のことを指しているわけではありません。 具体的にはこういうものを指しています。

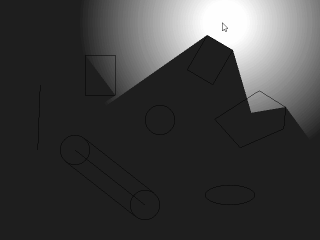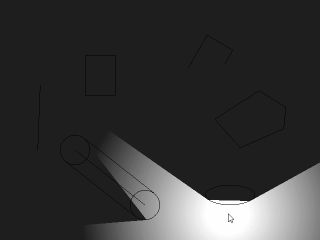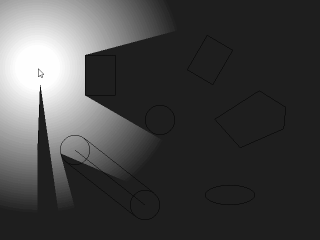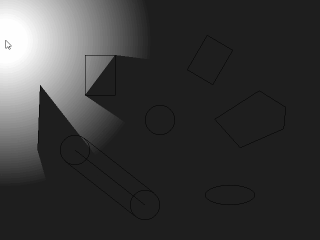
　この実装サンプルは、「d2cモジュール（HSP3専用）」で配布中ですので、興味ある方はどうそ。 右の図は図形と影のいち関係を見やすくしたものです。

　さて、d2cモジュールで、影を作る機能を実装したわけですが、手元に整理した資料がないのでどういう考え方で実装したのかを忘れてしまいそうです。 完全に忘れる前の忘備録と技術的な興味をもたれている方のために、解説を残しておくことにしました。

影の作り方

　早速、d2cCreateShadowPolygon命令で実装している影の作り方について解説します。

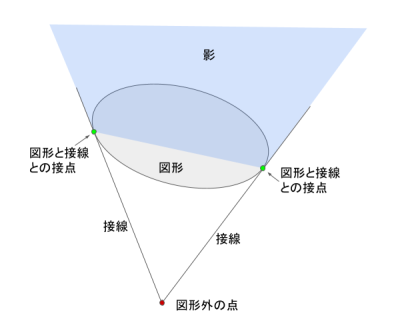
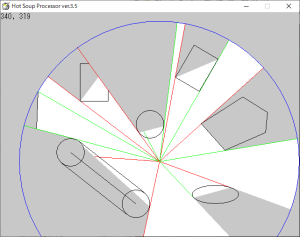
　影の作図はそれほど難しい仕組みではありません。 d2cm には図形に接線を引く命令を実装してあるので、これを使います。 この命令は、「図形外の点」（図の赤い丸）と「図形の情報（位置や形など）」（図の楕円部分）を設定すると、図形の輪郭線上に存在する「図形と接線との接点」2点（図の緑の丸）の座標を返します。 返された2点は、それぞれ図形外の点とで直線で結ぶと、図形外の点から図形に引いた接線を描くことができます。

　この「２接線の間」かつ「図形を境に図形外の点から遠い方」を黒く塗りつぶせば影（図の水色部分）ができます。 文章での説明が難しいで、図を見ていただけると分かりやすいと思います。

　図形の内側に影を描画していますが、影を描画した上に図形を描画すれば見えなくなるので気にしなくていいかなと思っています。

　説明したとおり、図形の高さの情報を使用していないので、影の長さにリアルさを出すことはできません。 遮蔽物の高さが光源よりも高いような場所をランタンひとつで探索する…という状況の演出には向いていますが、影の長さが有限になってしまうような遮蔽物の背が低い状況での使用には向いていません。 影としての利用にこだわらず、視界を可視化したものととして捉えて使ってもいいと思います。むしろこっちのほうが適切な使い方だと思います。

円の接線

　影の作成には接線が必要です。 d2cm では、接線を計算するための関数d2cTangentOf～を実装しているので、実装方法について説明していきます。

図形の形によって実装方法が少し異なるので、円の場合から解説していきます。

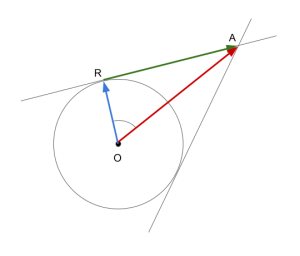
説明のため、記号を次のように定義します。
O : 円の中心点
A : 円外の点
R : 接線と円が接する点　←求めたい点！
ベクトルOA : 既知。
ベクトルOR : 長さが円の半径で、方向がわからない。
ベクトルRA : 長さも方向もわからない。

まず図から、次のことがわかります。

sin(∠AOR) = |RA| / |OA|
cos(∠AOR) = |OR| / |OA|

　|OA|と|OR|は、どちらのベクトルも長さがわかっているので、ベクトルのx成分とy成分を2乗してルートをとれば出てきますね。 |OA|と|OR|がわかれば、同様に|RA|もわかります。

|RA|= sqrt(|OA|^2 + |OR|^2)

これで、sin(∠AOR)とcos(∠AOR)がわかりました。

　ここまでわかれば簡単で、ベクトルOAの長さを円の半径と同じにし、±sin(∠AOR)、cos(∠AOR)で点Rの位置に回転させてあげればベクトルORを求めることができます。 回転させるの式はこんな感じのやつです。
X1 = X0 * cos(θ) - Y0 * sin(θ)
Y1 = Y0 * cos(θ) + X0 * sin(θ)

2次元なのでこれで問題なく算出できます。3次元の場合はどうすればいいんだろう…わかりません。

楕円の接線

　楕円の場合は、すべての縦横比を調整してあげれば円と点の接線にすることができます。 あとは円の場合と同じです。計算結果を元の縦横比に戻せばほしい結果を得られます。

カプセルの接線

　カプセルの両端は半円ですが、両端とも円と考えます。円が２個あるのでそれぞれ接線を算出します。 ４本接線が描けるので、その中から一番右にある線と左にある線を１本ずつ選ぶだけです。 左右の判定なので、比較には外積を使用します。

多角形の接線

　矩形も多角形も同じ方法で実装してあります。

　多角形は直線で構成されているので、接線が接触する点は多角形を構成する頂点のどれかであるというのが基本的な方針です。 辺は接点になりませんし、新しい頂点を作ったりもしません。図形を構成する頂点の中から接線が接する接点を探します。

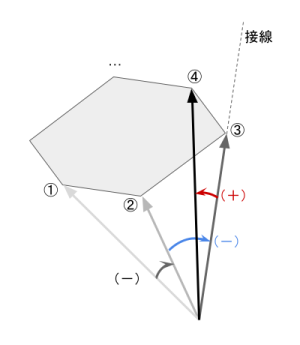
　図のように、図形外の点と図形の隣り合う2頂点を使って外積を計算します。 次に隣の辺の2頂点でも同じように外積を計算します。 図では、①×②、②×③、③×④、…という順番で外積を計算しています。 同様にして図形を１周分の計算を行います。

　計算結果を順に調べると、符号がマイナスからプラス、またはプラスからマイナスに変化する頂点が見つかります。 この頂点が図形の接線と接する頂点です。 図では、②×③の結果がマイナス、③×④の結果がプラスなので、③が図形の接線と接する頂点です。

　頂点は偶数個あり、凸多角形なら2つ、凹多角形なら4つ以上見つかるはずです。（もしかすると奇数のケースがあり得るかもしれませんが思いつきません。） 凹多角形の場合、図形の凹んだ部分の底の部分も検出されてしまいます。

　以上の手順から分かる通り、頂点数に比例して計算する回数が大きくなります。 普通はそんなにたくさんの頂点数を持った凸多角形を使うことはないと思うので、問題は起きないかなと思います。

凹多角形の影

　凹多角形の場合、検出した頂点を使って影を作成しようとしても簡単に影を作ることができません。 影を作る方の仕組みに工夫が必要なのですが、そこはまだ解決できていないので凹多角形への対応は見送っています。

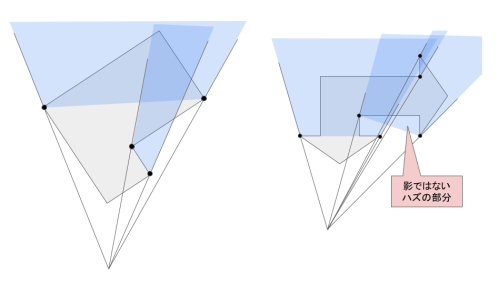
　例えば左のような図形なら対応する頂点を直線で結んで影を書けばいいので簡単です。 しかし、右のような図形の場合は、簡単には影が描けません。対応する頂点を直線で結ぶと、影になるはずの場所の一部が空白になったり、影がつかないはずの部分に影がついてしまったりします。

　2頂点間にある多角形の頂点座標データ（辺の形状）を使えばうまく描けそうな気もするのですが…未実装です。 実装できても描画が重くなりそうな予感がします。

まとめ

　まだ改良の余地ありの技術ですが、凸多角形のみに限定すれば手軽に影を描くことができます。 凹多角形の場合でも、複数に分割して凸多角形の集合にしてしまえば今の実装でも使えます。